11. 神经网络

11.1. 神经网络原理

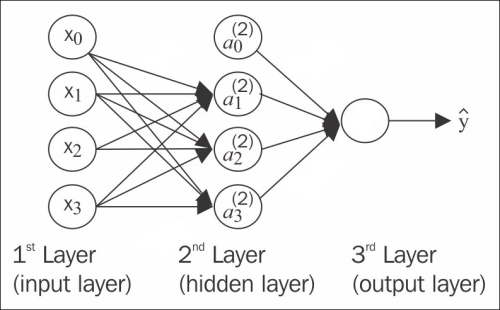
神经网络(Neural Networks)由多层感知器组成，每个节点的激活函数均使用 sigmoid 逻辑回归函数。

神经网络示意图

上图是一个简单的三层神经网络，输入层，1个隐藏层和一个输出层，每个神经节点和节点输出的权重均编号。其中：

• 层号从 1 编号，神经节点从 0 编号
• 层号使用上标加括号表示，节点号使用下标表示。例如 \(a^{(2)}_1\) 表示第 2 层的 1 号节点。同时它也用于表示节点的激活值。
• 0 号节点总是用来表示偏置单元（bias unit），对应感知器中的阈值，它没有输入，输出权重总为 1。
• 输出权重 \(w^{(l)}_{ji}\) 表示第 l 层的第 i 个节点输出到第 l+1 层的第 j 节点权重。显然这里的 ji 不是按照从左到右的层排序的，而是 l+1 节点在前，l 节点在后，这是为了矩阵表达时的方便才如此定义的，看到 ji 就明白是反向定义即可。

\(w^{(1)}_{23}\) 表示第 1 层上的节点 3 (即图中 \(a^{(1)}_3\) )输出到第 2 层上的节点 2 (即图中 \(a^{(2)}_2\) )的权重。

通常只有单个隐藏层的神经网络被称为单层或者浅层（Shallow）神经网络，当隐藏层大于一层时，被称为深度神经网络(Deep Neural Networks)。

神经网络的学习过程如下：

• 从输入层开始，通过网络前向传播（从左向右，也称为正向传播，Forward propagation）训练数据中的模式，以生成输出。
• 基于输出层的输出，通过一个代价函数计算所需最小化的误差。
• 反向传播（Back propagation）误差，通过链式法则计算代价函数对于网络中每个权重的导数，并更新模型。

每个节点（神经元）可以看作是返回值位于[0,1]连续区间上的逻辑回归单元。

以上图为例，可以写出第 2 层各节点的输入值

\[\begin{split}\begin{eqnarray} a^{(2)}_1 & = & \phi (z^{(2)}_1) & = & \phi (w^{(1)}_{10} x_0 + w^{(1)}_{11} x_1 + w^{(1)}_{12} x_2 + w^{(1)}_{13} x_3) \\ a^{(2)}_2 & = & \phi (z^{(2)}_2) & = & \phi (w^{(1)}_{20} x_0 + w^{(1)}_{21} x_1 + w^{(1)}_{22} x_2 + w^{(1)}_{23} x_3) \\ a^{(2)}_3 & = & \phi (z^{(2)}_3) & = & \phi (w^{(1)}_{30} x_0 + w^{(1)}_{31} x_1 + w^{(1)}_{32} x_2 + w^{(1)}_{33} x_3) \end{eqnarray}\end{split}\]

可以看到每一层的 a 都是由上一层所有的 x 和每一个 x 所对应的权重系数决定的。这种从左到右的算法就是前向传播算法(Forward propagation)。

其中：

\[\begin{eqnarray} \phi (z) & = & sigmoid(z) & = & \frac{1}{1+e^{-z}} \end{eqnarray}\]

观察上式，权重 w 和输入 x 可以写成矩阵点乘形式：

\[\begin{split}\begin{eqnarray} \mathbf{W^{(1)}} = \left( \begin{array}{ccc} w^{(1)}_{10} & w^{(1)}_{11} & w^{(1)}_{12} & w^{(1)}_{13} \\ w^{(1)}_{20} & w^{(1)}_{21} & w^{(1)}_{22} & w^{(1)}_{23} \\ w^{(1)}_{30} & w^{(1)}_{31} & w^{(1)}_{32} & w^{(1)}_{33} \end{array} \right) \end{eqnarray}\end{split}\]

\[\begin{split}\begin{eqnarray} \mathbf{x^{(1)}} = \left( \begin{array}{ccc} 1 \\ x_1 \\ x_2 \\ x_3 \end{array} \right) \end{eqnarray}\end{split}\]

其中权重矩阵 w 行数为第 2 层节点数（接受输出的节点数，不含偏置单元），列数为第 1 层节点数（所有输出节点数，含偏置单元）。观察每个权重的下编号，就可理解为何 l+1 节点在前，l 节点在后的编号定义了。

于是得出第 2 层输出的矩阵表示形式：

\[\begin{split}\begin{eqnarray} z^{(2)} & = & \mathbf{W^{(1)}} \mathbf{x^{(1)}} \\ a^{(2)} & = & \phi (z^{(2)}) = \phi (\mathbf{W^{(1)}} \mathbf{x^{(1)}}) \end{eqnarray}\end{split}\]

这只是针对一个训练样本所进行的计算。如果要对整个训练集进行计算，需要将训练集特征矩阵进行转置，使得同一个实例的特征都在同一列里。

\[\begin{split}\begin{eqnarray} \mathbf{X^{(1)}} = \left( \begin{array}{ccc} 1 & x_{11} & x_{12} & x_{13} \\ 1 & x_{21} & x_{22} & x_{23} \\ 1 & x_{31} & x_{32} & x_{33} \\ \vdots & \vdots & \vdots & \vdots \end{array} \right) \end{eqnarray}\end{split}\]

\[\begin{split}\begin{eqnarray} z^{(2)} & = & \mathbf{W^{(1)}} {\mathbf{X^{(1)}}}^T \\ a^{(2)} & = & \phi (z^{(2)}) = \phi (\mathbf{W^{(1)}} {\mathbf{X^{(1)}}}^T) \end{eqnarray}\end{split}\]

显然，第 3 层的输入矩阵形式也容易写出。这非常易于编码实现。

11.2. 神经网络实战

实现基本的神经网络类并不复杂，它是多个逻辑回归节点的分层叠加。

# nn.py
class NN(object):
    def __init__(self, sizes, eta=0.001, epochs=1000, tol=None):
        '''
        Parameters
        ------------
        eta : float
          Learning rate (between 0.0 and 1.0)
        epochs: uint
          Training epochs
        sizes : array like [3,2,3]
          Passes the layers.
        '''
        self.eta = eta
        self.epochs = epochs
        self.num_layers = len(sizes)
        self.sizes = sizes
        self.tol = tol

        self.biases = [np.random.randn(l, 1) for l in sizes[1:]]
        self.weights = [np.random.randn(l, x) for x, l in zip(sizes[:-1], sizes[1:])]

这里定义一个 NN 神经网络类，并定义初始化函数，完成以下工作：

• sizes 参数是一个层数列表，例如 [2,3] 表示神经网络有 2 层，每层节点数分别为 2 和 3。
• biases 成员记录了每一层的偏置单元的权重值，由于前一层偏置的权重个数等于后一层接受输出的节点数，所以这里取 sizes[1:]。
• weights 成员是权重列表，每一个元素都是一个 2 维的 ndarray，由于列表索引从 1 开始，所以 weights[0] 表示的是层 1->2 的权重矩阵。如果 1 层节点数为 2，2 层节点数为 3，则 weights[0] 就是一个 3*2 的二维矩阵。
• tol 停止条件的容忍度，当代价函数小于该值时，退出循环。

注意：理解 weights 的构造形式非常重要。为了逻辑更清晰，这里将偏置从权重矩阵中分离出来，同时初始化为 0-1 之间的随机正态分布数值。

    def sigmoid(self, z):
        return 1.0/(1.0 + np.exp(-z))

    def sigmoid_derivative(self, z):
        sg = self.sigmoid(z)
        return sg * (1.0 - sg)

sigmoid 为激活函数，sigmoid_derivative 对应它的导数，它被用于梯度下降算法中，其中的临时变量 sg 可以减少一次 sigmoid 运算。

    def feedforward(self, X):
        X = X.T
        for b, W in zip(self.biases, self.weights):
            X = self.sigmoid(np.dot(W, X) + b)
        return X

实现前向传播算法(Forward propagation)函数，关键点是从第一层开始针对每一层进行权重矩阵求和然后做 sigmoid。另外注意到 X 是一个训练集的输入矩阵，每一行代表一个样本，所以传入参数后要先对其转置。

显然返回值就是最后的节点输出，它是一个二维矩阵，如果输出节点数为 n，输入样本数为 m，那么它的 shape 为 (n,m)，第 i 行对应第 i 个节点上的输出，第 j 列对应第 j 个样本通过神经网络处理的输出，所以 ij 个元素对应第 j 个样本在节点 i 上的输出（这里 i 和 j 下标均从 0 开始）。

这里使用异或训练集来查看 feedforward 函数的输出：

def boolXorTrain():
    # Bool xor Train         x11 x12 y1
    BoolXorTrain = np.array([[1, 0, 1],
                             [0, 0, 0],
                             [0, 1, 1],
                             [1, 1, 0]])
    X = BoolXorTrain[:, 0:-1]
    y = BoolXorTrain[:, -1]

    nn = NN([2,2,1])
    a = nn.feedforward(X)
    print(a.shape)

boolXorTrain()

>>>
(1, 4)

这里使用了 4 个训练样本，网络层数为 [2,2,1]，输出节点数为 1，所以 feedforward 函数会输出 1 行 4 列的结果，这和理论分析是一致的。

从算法上看，feedforward 就是在对输入通过网络权重计算输出的过程，也就是算法进行预测的过程。预测函数也就可以如下实现了：

  def predict(self, X):
      ff = self.feedforward(X)
      if self.sizes[-1] == 1: # 1 output node
          return np.where(ff >= 0.5, 1, 0)

      return np.argmax(ff, axis=0)

这里的预测函数同时考虑到了输出节点只有 1 个和多个的情况：

• 如果输出节点只有 1 个，就是一个二分类神经网络，预测方式和逻辑回归是一致的，结果为 0 或 1。
• 如果输出节点有 n (n>1) 个，那么就是 n 分类算法，此时取输出层中输出似然概率最高的那个节点，每个分类编号从 0 到 n - 1。

在多分类情况下，n 个分类通常会安排 n 个输出节点，尽管 n 个节点从输出二进制（sigmoid输出经阈值处理后总是输出0,1）上可以表示 2^n 种分类，这是基于经验主义规定的，或许是 n 个输出节点增加了整个网络参数的节点数和权重数目，使得分类效果更好。

到这里我们还缺少最核心的东西，基于梯度下降的训练函数 fit。在实现它之前必须再次回顾逻辑回归的代价函数和梯度下降算法，因为神经网络本质上就是多层逻辑回归模型的叠加。

11.3. 反向传播理论推演

逻辑回归是一个二分类算法，回顾它的代价函数：

\[J(w) = \sum_{i=1}^{n}-y^i\ln {(\phi (z^i))}-(1-y^i)\ln {(1-\phi (z^i))}\]

逻辑回归算法，一个输入 \(x^i\) 只对应一个输出 \(y^i\)，可以看做是一个标量，对应的标签值为 0 或者 1。但是在神经网络中，可以有很多输出变量，也即 K 个分类对应一个 K 维的向量，对应不同的标签向量。例如 3 分类的标签向量可能为：

\[\begin{split}\begin{eqnarray} \mathbf{y^i} = \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right) \left( \begin{array}{ccc} 0 \\ 1 \\ 0 \end{array} \right) \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \end{array} \right) \end{eqnarray}\end{split}\]

那么，对于 K 分类，标签向量被记为 \(y^i_k\)，k 取 1 到 K。此时的代价函数可表示为多个输出节点的代价函数和：

\[J(w) = \sum_{i=1}^{n}\sum_{k=1}^{K}-y^i_k {\ln {(\phi (z^i))}}_k - (1-y^i_k) {\ln {(1-\phi (z^i))}}_k\]

尽管表达式看起来很复杂，实际算法上只不过在外循环内加上一个用于计算每个输出节点在训练样本 \(x^i\) 上代价的累加。

相较于上面的形式，笔者更喜欢把 K 累加放在外边，这样内侧累加就和逻辑回归代价函数保持一致，表示一个输出节点上的代价函数：

\[J(w) = \sum_{k=1}^{K} \sum_{i=1}^{n} -y^i_k{\ln {(\phi (z^i))}}_k - (1-y^i_k) {\ln {(1-\phi (z^i))}}_k\]

在逻辑回归中只要对代价函数求权重偏导，就可以得到调整权重 \(\Delta w\)，但是神经网络具有多层，需要采用一种反向传播算法，也即先计算最后一层的误差（预测值与标签值的差），然后再一层一层反向求出各层的误差，直到倒数第二层。

理解反向传播的第一个关键点在于实际上它是逐个对每个训练样本计算代价函数的关于各个权重的偏导，并调整权重（实际上就是随机梯度下降），这将问题大大简化，我们无需一次考虑代价函数中的两层累加，而把问题的注意力放在单个训练样本对代价函数的影响上。

反向传播（对第 2 层权重求偏导）

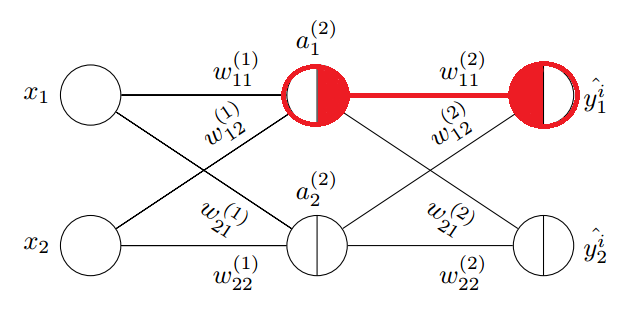
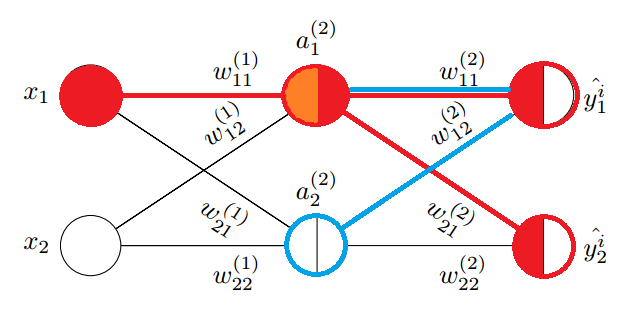
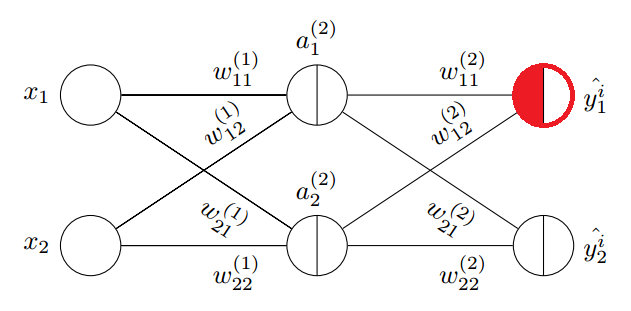
上图中是一个三层的神经网络，每层均有 2 个节点，暂不考虑偏置节点。除了输入节点外，每个节点被分割为左右两个半圆，左边表示节点的加权求和的权重输入，右边表示节点的激活输出。观察上图中的红色圈中的输出层节点 \(a^{(3)}_{1}\) ，它的权重输入通常标记为 \(z^{(3)}_{1}\); 它的输出与节点编号相同：\(a^{(3)}_{1}=\hat{y^i_1}\)，这是当样本 i 输入到神经网络后，节点 \(a^{(3)}_{1}\) 的输出。

我们从图中被涂成红色的边上的权重 \(w^{(2)}_{11}\) 开始考虑如何对它进行调整，以使得输出的代价函数最小。 这条边的输入部分就是它连接的左侧节点 \(a^{(2)}_{1}\) 的输出，所以把 \(a^{(2)}_{1}\) 节点的右半边涂成红色， 这条边的权重输出对应到它连接的右侧节点 \(a^{(3)}_{1}\) 的输入 \(z^{(3)}_{1}\) ，所以把它的左半边涂成红色。

我们很快就会明白为何把这两个半圆涂成红色，这是某种强烈的隐喻，边上权重的调整与它们息息相关。

为了计算 \(w^{(2)}_{11}\) 的偏导数，就要理清 \(w^{(2)}_{11}\) 是如何影响代价函数的，这样我们就可以使用链式法则求偏导了。

\[\begin{eqnarray} J(w) & = & -y^i_1 {\ln {(\phi (z^{(3)}_1))}} - (1-y^i_1) {\ln {(1-\phi (z^{(3)}_1))}} \end{eqnarray}\]

观察关于训练样本 i 的代价函数，注意到式子中的 \(\phi (z^{(3)}_1)\)，它就是输出层节点的输出：

\[\begin{eqnarray} a^{(3)}_1 & = & \phi (z^{(3)}_1) &=& \hat{y^i_1} \end{eqnarray}\]

与权重变量 \(w^{(2)}_{11}\) 发生关联的就是 \(z^{(3)}_1\)：

\[\begin{eqnarray} z^{(3)}_1 & = & w^{(2)}_{11} a^{(2)}_1 + w^{(2)}_{12} a^{(2)}_2 \end{eqnarray}\]

由以上各式根据链式法则求对 \(w^{(2)}_{11}\) 的偏导：

\[\frac {\partial {J(w)}} {\partial {w^{(2)}_{11}}} = \frac {\partial {J(w)}} {\partial a^{(3)}_{1}} \frac {\partial a^{(3)}_{1}} {\partial z^{(3)}_{1}} \frac {\partial z^{(3)}_{1}} {\partial {w^{(2)}_{11}}}= \frac {\partial {J(w)}} {\partial {\phi (z^{(3)}_1)}} \frac {\partial {\phi (z^{(3)}_1)}} {\partial z^{(3)}_{1}} \frac {\partial z^{(3)}_{1}} {\partial {w^{(2)}_{11}}}\]

观察以上公式，它分为左右两个部分，左侧部分对应代价函数对权重右侧节点的输入的偏导，右侧部分对应权重左侧节点的输出，当然左右可以交换下位置，这样就和图中的标记顺序一致了。到这里就可以理解为何图中如此涂色了。

通常代价函数对节点输入的偏导数称为该节点的误差信号（Error Signal），记为 \(\delta^{(l)}_i\)，它表示当这个节点的输入变化 \(\Delta z\) 时，代价函数将产生 \(\delta^{(l)}_i\Delta z\) 的误差（实际上这就是对导数的数学意义的解释）。这里称为误差信号，更准确的意思是对代价函数的误差的影响大小，信号越大（越强），节点上的输入变化导致的误差就越大。

这里参考逻辑回归中的求导过程，上式结果为：

\[\frac {\partial {J(w)}} {\partial {w^{(2)}_{11}}} = (a^{(3)}_1-{y^i_1})a^{(2)}_1 = a^{(2)}_1(a^{(3)}_1-{y^i_1}) \qquad (0)\]

同理，根据上述规则，考虑所有输出节点的代价函数对第 2 层各权重的偏导关系，可以得出：

\[\begin{split}\begin{eqnarray} \frac {\partial {J(w)}} {\partial {w^{(2)}_{12}}} & = & a^{(2)}_2(a^{(3)}_1-{y^i_2}) \qquad (1)\\ \frac {\partial {J(w)}} {\partial {w^{(2)}_{21}}} & = & a^{(2)}_1(a^{(3)}_2-{y^i_2}) \qquad (2)\\ \frac {\partial {J(w)}} {\partial {w^{(2)}_{22}}} & = & a^{(2)}_2(a^{(3)}_2-{y^i_2}) \qquad (3) \end{eqnarray}\end{split}\]

观察以上四个偏导公式，我们对偏导的两部分顺序进行了交换，这就和图中的左右顺序一致了：左侧部分对应权重节点的输入，右侧部分对应 \(\delta^{(3)}_i\)。如果考虑所有第三层的节点，就可以把误差写成向量的形式，记作 \(\delta^{(3)}\) ：

\[\begin{split}\begin{eqnarray} \mathbf{\delta^{(3)}} = \left( \begin{array}{ccc} a^{(3)}_1 - y^i_1 \\ a^{(3)}_2 - y^i_2 \end{array} \right) \end{eqnarray}\end{split}\]

同时针对第二层的权重的偏导公式可以写成如下形式，注意其中是向量逐元素相乘。

\[\begin{eqnarray} \frac {\partial {J(w)}} {\partial {w^{(2)}_{ij}}} & = {a^{(2)}_j} \delta^{(3)}_i \qquad (1.1) \end{eqnarray}\]

观察上式中的下标关系，可以写成矩阵的乘法形式：

\[\begin{split}\begin{eqnarray} \frac {\partial {J(w)}} {\partial {w^{(2)}}} = \left( \begin{array}{ccc} \delta^{(3)}_1 \\ \delta^{(3)}_2 \end{array} \right) \left( \begin{array}{ccc} a^{(2)}_1 & a^{(2)}_2 \end{array} \right) \end{eqnarray}=\delta^{(3)} {a^{(2)}}^T\end{split}\]

尽管已经发现了代价函数对权重的偏导规律：输入和信号误差相乘。但是假如每一层的信号误差都要使用链式法则重新计算（特别是层数很多时），那么计算量无疑是巨大的，观察链式法则，我们会发现对第 1 层求偏导的计算链要基于第 2 层的信号误差，同理第 2 层的信号误差要基于第 3 层的信号误差，直至输出层。

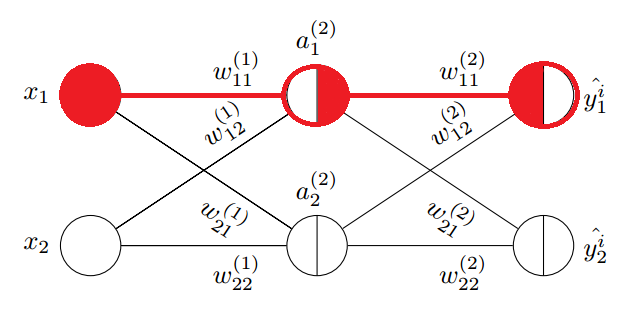
这里继续对第 1 层中权重 \(w^{(1)}_{11}\) 求偏导，来说明以上的规律。

反向传播（对第 1 层权重求偏导）

图中输入层无需考虑加权和激活部分，直接输入到权重边，所以整个圆被涂红。首先梳理清楚 \(w^{(1)}_{11}\) 与代价函数的关系（函数链，以便运用链式求导法则）：

\[\begin{split}\begin{eqnarray} z^{(2)}_1 & = & w^{(1)}_{11} x^1 + w^{(1)}_{12} x^2 \\ a^{(2)}_1 & = & \phi({z^{(2)}_1})\\ z^{(3)}_1 & = & w^{(2)}_{11} a^{(2)}_1 + w^{(2)}_{12} a^{(2)}_2 \\ z^{(3)}_2 & = & w^{(2)}_{21} a^{(2)}_1 + w^{(2)}_{22} a^{(2)}_2 \end{eqnarray}\end{split}\]

显然它通过 \(z^{(3)}_1\) 和 \(z^{(3)}_2\) 与代价函数关联了起来（这里的代价函数就要考虑所有输出点的情况了），另外我们在对第二层权重求偏导时，已经计算过代价函数对 \(z^{(3)}_1\) 和 \(z^{(3)}_2\) 的偏导，即 \(\delta^{(3)}_1\) 和 \(\delta^{(3)}_2\)，所以对 \(w^{(1)}_{11}\) 的偏导公式可以写成：

\[\frac {\partial {J(w)}} {\partial {w^{(1)}_{11}}} = (\frac {\partial {J(w)}} {\partial {\phi (z^{(3)}_1)}} \frac {\partial {\phi (z^{(3)}_1)}} {\partial z^{(3)}_{1}} \frac {\partial z^{(3)}_{1}} {\partial {\phi (z^{(2)}_1)}} + \frac {\partial {J(w)}} {\partial {\phi (z^{(3)}_2)}} \frac {\partial {\phi (z^{(3)}_2)}} {\partial z^{(3)}_{2}} \frac {\partial z^{(3)}_{2}} {\partial {\phi (z^{(2)}_1)}}) \frac {\partial {\phi (z^{(2)}_1)}} {\partial {z^{(2)}_{1}}} \frac {\partial {(z^{(2)}_2)}} {\partial {w^{(1)}_{11}}}\]

我们把 \(\delta^{(3)}_1\) 和 \(\delta^{(3)}_2\) 代入以上公式，上式被化简成：

\[\frac {\partial {J(w)}} {\partial {w^{(1)}_{11}}} = x^1(\delta^{(3)}_1 w^{(2)}_{11} + \delta^{(3)}_2 w^{(2)}_{21}) \frac {\partial {\phi (z^{(2)}_1)}} {\partial {z^{(2)}_{1}}}\]

注意这里把输入 \(x^1\) 放在了最左边，其中：

\[\frac {\partial {\phi (z^{(2)}_1)}} {\partial {z^{(2)}_{1}}} = a^{(2)}_1(1-a^{(2)}_1)\]

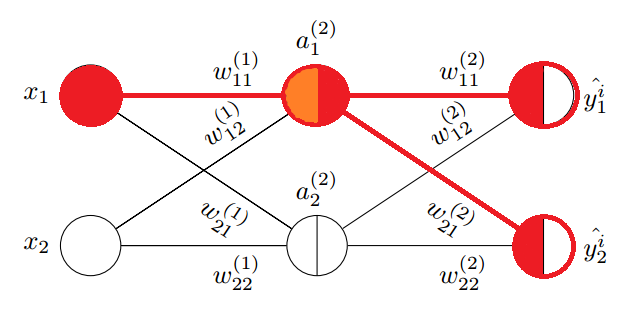
我们不急于写出其他几个权重的偏导数，而是观察上式与第 2 层权重偏导公式(1.1)的关系，左边为输入项，右侧为代价函数对 \(z^{(2)}_1\) 的偏导，根据误差信号的定义，右侧部分可以标记为 \(\delta^{(2)}_1\)，对应下图中的橙色部分的偏导。

\[\delta^{(2)}_1 = (\delta^{(3)}_1 w^{(2)}_{11} + \delta^{(3)}_2 w^{(2)}_{21}) \frac {\partial {\phi (z^{(2)}_1)}} {\partial {z^{(2)}_{1}}}\]

反向传播（第 2 层信号误差）

对照上图，仔细观察 \(\delta^{(2)}_1\) 组成的各个部分，可以体会到它和正向传播的某种对称性。

反向传播和正向传播关系

观察图中蓝色部分，正向传播使用权重矩阵点乘输入进行：

\[\begin{split}\begin{eqnarray} \mathbf{W^{(2)}} = \left( \begin{array}{ccc} w^{(2)}_{11} & w^{(2)}_{12} \\ w^{(2)}_{21} & w^{(2)}_{22} \end{array} \right) \end{eqnarray}\end{split}\]

\[\begin{split}\begin{eqnarray} \mathbf{a^{(2)}} = \left( \begin{array}{ccc} a^{(2)}_{1}\\ a^{(2)}_{2} \end{array} \right) \end{eqnarray}\end{split}\]

\[z^{(3)} = {\mathbf{W^{(2)}}} \mathbf{a^{(2)}}\]

为何观察上述对称性，我们把 \(\delta^{(2)}\) 的两个表达式列出来：

\[\begin{split}\begin{eqnarray} \delta^{(2)}_1 &=& (\delta^{(3)}_1 w^{(2)}_{11} + \delta^{(3)}_2 w^{(2)}_{21}) \frac {\partial {\phi (z^{(2)}_1)}} {\partial {z^{(2)}_{1}}} \\ \delta^{(2)}_2 &=& (\delta^{(3)}_1 w^{(2)}_{12} + \delta^{(3)}_2 w^{(2)}_{22}) \frac {\partial {\phi (z^{(2)}_2)}} {\partial {z^{(2)}_{2}}} \end{eqnarray}\end{split}\]

观察上述矩阵运算过程，正向传播使用权重矩阵的各行与输入相乘叠加得出下一层的权重输入，逆向传播使用权重矩阵的各列分别信号误差相乘，得出上一层的信号误差，所以 \(\delta^{(2)}\) 和 \(\delta^{(3)}\) 的关系可以表示为：

\[\delta^{(2)} = {\mathbf{W^{(2)}}}^T \delta^{(3)} \odot \frac {\partial {\phi (z^{(2)})}} {\partial {z^{(2)}}}\]

其中 \(\odot\) 表示元素逐项对应相乘。图中的蓝色线对应权重矩阵的第一行，红色线对应权重矩阵的第一列，它们可以同时充当正向传播和反向传播的桥梁，也即转置的作用。到这里就可以总结出反向传播的所有公式了：

\[\delta^{(l)} = {{\mathbf{W}}^{(l)}}^T \delta^{(l+1)} \odot \frac {\partial {\phi (z^{(l)})}} {\partial {z^{(l)}}} \qquad (0)\]

注意当计算到第 2 层的信号误差时，第 1 层的权重调整系数就已经得到了，所以式子中的 l >= 2，并且当 l 为输出层时，无需激活函数的偏导部分，l 的取值范围为 [L,2]。有了每层的误差，就可以基于它计算每个权重的调整系数了，它是对式 (1.1) 的扩展：

\[\begin{eqnarray} \frac {\partial {J(w)}} {\partial {w^{(l-1)}_{ij}}} & = {a^{(l-1)}_j} \delta^{(l)}_i = \delta^{(l)} {a^{(l-1)}}^T \qquad (1) \end{eqnarray}\]

显然这里使用 l-1 是为了公式 (1) 中 l 的取值范围和公式 (2) 保持一致。对于偏置项，由于输入总是 1， 所以调整系数就是输出节点的信号误差。

尽管这里只计算了 2 层权重的偏导来推导反向传播公式，显然它基于链式法则，可以推广到任意层，整个反向传播的计算流程描述如下：

• 随机初始化所有权重
• 使用一个样本进行正向传播，得到输出层的信号误差
• 复制一份权重和偏置，并初始化为 0，所有系数调整在该拷贝上进行
• 基于输出层的信号误差反向计算上一层的信号误差，使用信号误差计算出调整系数
• 对拷贝权重和偏置进行调整，直至计算到第 2 的信号误差并调整完第一层 1 的权重和偏置
• 更新拷贝项替到原权重和偏置

以上算法显示是随机梯度下降，也可以使用批量梯度下降，也即使用一批样本，对拷贝的权重和偏置进行累积调整，这一批训练样本处理完后再更新到原权重和偏置，这样效率要高很多。

11.3.1. 反向传播理论思考

反向传播是如何被发现的？是偶然的，还是必然的。我记起来孟德尔发现遗传定律的豌豆杂交实验。豌豆具有多种特征：皮皱和光滑，高矮，种子颜色，种子的圆扁等等，它们之间有无数种组合，这里很像多个训练样本对层层线性和非线性神经网络的影响。

孟德尔成功的原因有几个要点：

• 将问题简化，先研究一对相对性状的遗传，再研究两对或多对性状的遗传
• 应用统计学方法对实验结果进行分析
• 基于对大量数据的分析而提出假设，再设计实验来验证。

格雷戈尔·孟德尔（Gregor Johann Mendel，1822年7月20日—1884年1月6日）

孟德尔在以上方法指导下（更可能是后人根据孟德尔实验成功的方法论总结），耐心地进行 7 年的豌豆种植试验，最终破解了生物遗传密码，被誉为遗传学之父（在被埋没 35 年之后）。

逆向传播的发现也具有类似特征：

• 首先简化问题：只考虑一个样本对一个输出节点的影响
• 运用链式法则求倒数第 1 层的权重偏导数，观察发现它只与左侧节点的输入和代价函数对右侧节点输入的偏导数（信号误差）有关，并且基于链式法则，对任意层有效。
• 继续对前一层求偏导，可以发现第 2 层的信号误差与第 3 层的信号误差的关系，进而总结出规律公式 (0) 和 (1)。

并且可以发现最后一层的信号误差与代价函数和激活函数有关，其他层信号误差只与后一层的信号误差以及激活函数（激活函数关于输入的偏导数）有关：

• 如果我们要替换代价函数，那么只要调整最后一层信号误差计算方式。
• 如果要替换激活函数，那么在计算每一层信号误差时都要考虑，当然我们把它和它的导数均定义为函数，在代码实现上非常简单。

在大部分教科书上，神经网络的代价函数可能使用的是 MSE（均方差），而不是 MLE（最大对数似然函数）。笔者猜测，如果对线性回归比较熟悉，那么就倾向于使用 MSE，至少从形式上看很简单，并且求导过程不会那么可怕；另一条研究神经网络的路线是：感知器到Adaline模型，到逻辑回归，再到神经网络，那么选择 MLE 就水到渠成。笔者更倾向于第二条路线。不过这无关紧要，重要的是不同的代价函数对神经网络实现和性能到底有什么影响？

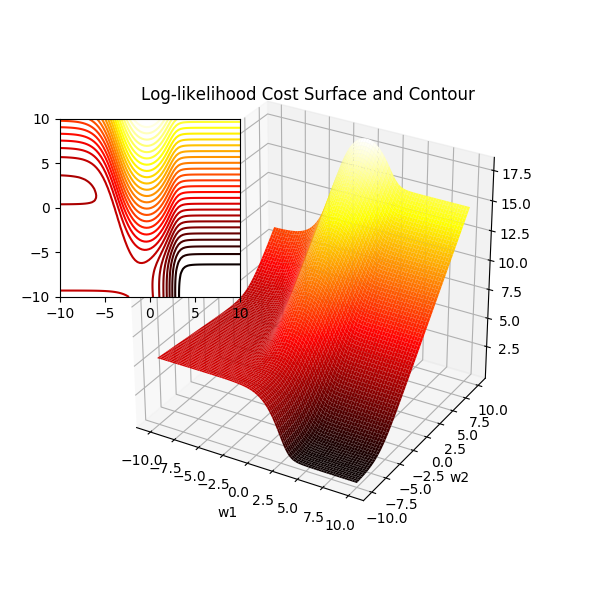
或许有人记得 MLE 形式的代价函数在逻辑回归中是个凸函数，这让我们可以找到极小值，而在神经网络中，每个权重都经过了层层的线性和非线性叠加变换，指望这里的代价函数具有凸函数特性是不可能的。想象一个层数为 [2，2，1]的神经网络，它的权重数目为 2*2 + 2*1 = 6，我们不可能绘制一个 6 维的代价函数曲面，但是我们可以把其中的 4 个权重固定，只改变其中的两个，这样取得的曲面图就是一个子集，它能从侧面反映出代价函数的凹凸性，所以我称为这里的代价函数曲面为拟曲面图。

下图是在 XOR 问题上训练完成的权重上，调整其中两个权重得到的曲面图，显然它不是凸面函数，有着丰富的波动从而导致众多的局部极小值。此图是在直观层面上说明选择神经网络的代价函数已经不再考虑凹凸性了，也即凹凸性不是选择 MLE 方法的原因。这里可以提及的是权重使用随机初值化，而不是全 0，是因为 0 附近很可能是一个局部极小值，导致每次迭代都无法收敛。

神经网络的代价函数拟曲面图

11.3.2. MSE 代价函数

MSE 代价函数很容易写出来，与 Adaline 模型不同的是，这里要考虑输出层有 K 个输出节点的情况，也即预测值是一个向量，而不再是一个数字：

\[J(w) = \frac{1}{2n}\sum_{i=1}^{n}\sum_{k=1}^{K}({\hat y}^i_k - {y^i_k})^2\]

反向传播MSE代价函数求偏导

上面已经指出如果要替换代价函数，那么只要调整最后一层信号误差计算方式。这里使用 MSE 代价函数对上图中的 \(z^{(3)}_1\) 求偏导数，在考虑一个样本情况时可忽略常数 1/n：

\[\frac {\partial {J(w)}} {\partial {z^{(3)}_{1}}} = \frac {\partial {J(w)}} {\partial a^{(3)}_{1}} \frac {\partial a^{(3)}_{1}} {\partial z^{(3)}_{1}}= \frac {\partial {J(w)}} {\partial {\phi (z^{(3)}_1)}} \frac {\partial {\phi (z^{(3)}_1)}} {\partial z^{(3)}_{1}}= ({\hat y}^i_1 - {y^i_1})\frac {\partial {\phi (z^{(3)}_1)}} {\partial z^{(3)}_{1}} = (a^{(3)}_1 - {y^i_1})\frac {\partial {\phi (z^{(3)}_1)}} {\partial z^{(3)}_{1}}\]

得到最后一层的信号误差 \(\delta^{(3)}\)：

\[\begin{split}\begin{eqnarray} \mathbf{\delta^{(3)}} = \left( \begin{array}{ccc} (a^{(3)}_1 - y^i_1)\frac {\partial {\phi (z^{(3)}_1)}} {\partial z^{(3)}_{1}} \\ (a^{(3)}_2 - y^i_2)\frac {\partial {\phi (z^{(3)}_2)}} {\partial z^{(3)}_{2}} \end{array} \right) \end{eqnarray}\qquad (MSE)\end{split}\]

对比最大对数似然估计，可以看到这里只是多了激活函数对节点输入的偏导数项。显然 MSE 在反向计算每一层信号误差时都需要加入该项，则 MLE 在计算最后一层信号误差时无需考虑（因为代价函数求导时约去了该项）。

\[\begin{split}\begin{eqnarray} \mathbf{\delta^{(3)}} = \left( \begin{array}{ccc} a^{(3)}_1 - y^i_1 \\ a^{(3)}_2 - y^i_2 \end{array} \right) \end{eqnarray}\qquad (MLE)\end{split}\]

基于以上理论，实现反向传播不再困难，我们尝试在一个样本上实现反向传播算法，并在测试验证正确后再尝试优化。

11.3.3. 实现反向传播

定义名为 backprop 的类函数，x 是一个样本，为 1*n 的特征矩阵。y 是标签值，它是一个 K 维向量，K 为输出层的节点数。

  def backprop(self, x, y):
      # 初始化新的偏置和权重系数矩阵
      delta_b = [np.zeros(b.shape) for b in self.biases]
      delta_w = [np.zeros(w.shape) for w in self.weights]

      # 转置样本特征矩阵，以便于权重矩阵左乘
      x = x.reshape(x.shape[0], 1)
      y = y.reshape(y.shape[0], 1)
      activation = x

      # 记录每一层每一节点的激活函数输出，用于在反向传播时计算激活函数的偏导 a(1-a)
      # 第一层就是 x 自身
      acts = [x]

      # zs 记录每一层每一节点的权重输入
      zs = []

      # 进行前向传播，以得到每层每个节点的权重输入，激活函数值和最终输出层的信号误差
      for b, W in zip(self.biases, self.weights):
          z = W.dot(activation) + b
          zs.append(z)
          activation = self.sigmoid(z)
          acts.append(activation)

      # 反向传播，这里使用 MSE 代价函数，所以 L-1 层信号误差计算需乘以激活函数的导数
      delta = (acts[-1] - y) * self.sigmoid_derivative(zs[-1])
      delta_b[-1] = delta   # 偏置的输入总是 1， 所以就是信号误差
      delta_w[-1] = np.dot(delta, acts[-2].transpose())
      for l in range(2, self.num_layers):
          sp = self.sigmoid_derivative(zs[-l])
          delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
          delta_b[-l] = delta
          delta_w[-l] = np.dot(delta, acts[-l-1].transpose())

      # 更新偏置和权重
      self.biases = [b-(self.eta) * nb / X.shape[0]
                      for b, nb in zip(self.biases, delta_b)]
      self.weights = [w-(self.eta) * nw / X.shape[0]
                      for w, nw in zip(self.weights, delta_w)]

结合理论分析，再理解上面的代码实现并不困难。注意以上函数一次只使用一个样本进行权重调整，这在实际中运行中效率很慢，我们可以使用矩阵来实现批量样本的权重更新。

  # X is an array with n * m, n samples and m features every sample
  def mbatch_backprop(self, X, y):
      delta_b = [np.zeros(b.shape) for b in self.biases]
      delta_w = [np.zeros(w.shape) for w in self.weights]

      # feedforward
      if X.ndim == 1:
          X = X.reshape(1, X.ndim)
      if y.ndim == 1:
          y = y.reshape(1, y.ndim)

      activation = X.T
      acts = [activation]
      zs = []
      for b, W in zip(self.biases, self.weights):
          z = W.dot(activation) + b
          zs.append(z)
          activation = self.sigmoid(z)
          acts.append(activation)

      # 这里的注意点在于偏置的更新，需要进行列求和
      delta = (acts[-1] - y.T) * self.sigmoid_derivative(zs[-1])
      delta_b[-1] = np.sum(delta, axis=1, keepdims=True)
      delta_w[-1] = np.dot(delta, acts[-2].transpose())
      for l in range(2, self.num_layers):
          sp = self.sigmoid_derivative(zs[-l])
          delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
          delta_b[-l] = np.sum(delta, axis=1, keepdims=True)
          delta_w[-l] = np.dot(delta, acts[-l-1].transpose())

      self.biases = [b-(self.eta) * nb / X.shape[0]
                      for b, nb in zip(self.biases, delta_b)]
      self.weights = [w-(self.eta) * nw / X.shape[0]
                      for w, nw in zip(self.weights, delta_w)]

训练函数支持批量训练，这里默认批处理样本数为 8。

  # MSE 代价函数，用于统计观察下降情况
  def quadratic_cost(self, X, y):
      return np.sum((self.feedforward(X) - y.T)**2) / self.sizes[-1] / 2

  def fit_mbgd(self, X, y, batchn=8, verbose=False):
      '''mini-batch stochastic gradient descent.'''
      self.errors_ = []
      self.costs_ = []
      self.steps_ = 100  # every steps_ descent steps statistic cost and error sample

      if batchn > X.shape[0]:
          batchn = 1

      for loop in range(self.epochs):
          X, y = scaler.shuffle(X, y) # 每周期对样本随机处理
          if verbose: print("Epoch: {}/{}".format(self.epochs, loop+1), flush=True)

          x_subs = np.array_split(X, batchn, axis=0)
          y_subs = np.array_split(y, batchn, axis=0)
          for batchX, batchy in zip(x_subs, y_subs):
              self.mbatch_backprop(batchX, batchy)

          # 使用正向传播获取误差值，计算代价函数值，观察收敛情况
          if self.complex % self.steps_ == 0:
              cost = self.quadratic_cost(X,y)
              self.costs_.append(cost)

              # 平均最后5次的下降值，如果下降很慢，停止循环，很可能落入了局部极小值
              if len(self.costs_) > 5:
                  if sum(self.costs_[-5:]) / 5 - self.costs_[-1] < self.tol:
                      print("cost reduce very tiny less than tol, just quit!")
                      return

              print("costs {}".format(cost))
          self.complex += 1

注意，如果下降很慢，则停止循环，很可能落入了局部极小值，此时应该重新训练网络以尝试其他权重值。

11.3.4. 分割异或问题

我们尝试用最简单的 [2,2,1] 神经网络来解决 XOR 异或分割问题。众所周知，异或问题不是线性可分的，那么神经网络是怎么通过非线性函数实现异或分割的呢？

def boolXorTrain():
    # Bool xor Train         x11 x12 y1
    BoolXorTrain = np.array([[1, 0,  1],
                             [0, 0,  0],
                             [0, 1,  1],
                             [1, 1,  0]])
    X = BoolXorTrain[:, 0:2]
    y = BoolXorTrain[:, 2]
    if y.ndim == 1: # vector to 2D array
        y = y.reshape(y.shape[0], 1)

    nn = NN([2,2,1], eta=0.5, epochs=10000, tol=1e-4)
    nn.fit_mbgd(X,y)
    pred = nn.predict(X)
    print(nn.weights)
    print(pred)

如果我们尝试将权重和偏置的初始值均置为 0，将会诧异地发现根本无法收敛。这预示着 0 点处是一个局部极小点，实际使用中如果发现跌入局部极小点而无法收敛到 0 附近，那么就要重新随机初始化权重，再进行模型训练。

>>> python nn.py
......
costs 0.00024994697604848544
cost reduce very tiny, just quit!
weights: [array([[-5.55203673,  5.34505725],
       [-6.10271765,  6.20215693]]), array([[ 9.2106689 , -8.70927677]])]
biases: [array([[-2.89311115],
       [ 3.10518764]]), array([[ 4.06794821]])]
[[1 0 1 0]]

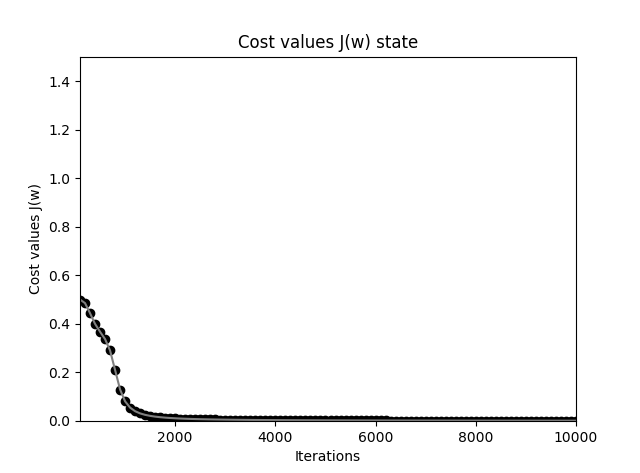
实际观察，在学习率为 0.5 时，大约需要 7000 个迭代周期（实际上由于样本很少，等同于批量梯度下降）才会收敛到比较满意的值。当然我们可以增加 tol 来成倍降低迭代周期，当然我们最关心的不仅仅是计算量的大小，还有分类的实际效果。

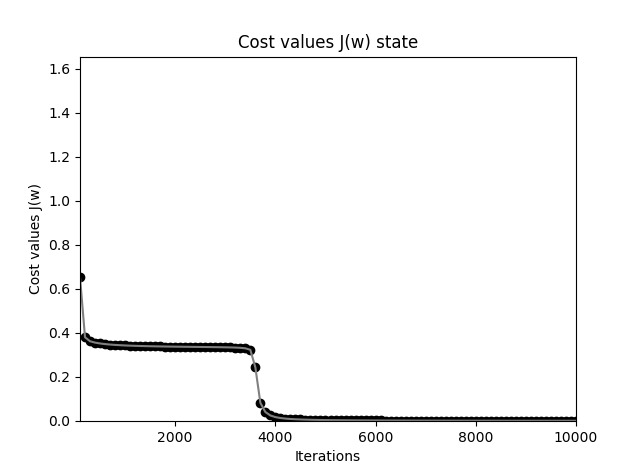
首先看下代价下降曲线图，首先很庆幸我们随机的一组权重参数在一开始就给出了较小的代价值，也即这次随机选择的点邻近最优点（也可能是局部最优点），在迭代大约 2000次之后，就已经下降到接近于 0。

神经网络在 XOR 问题上的代价函数下降曲线

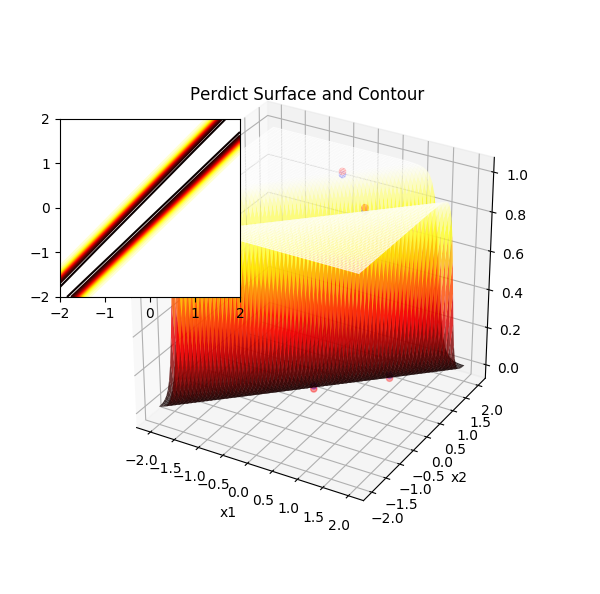
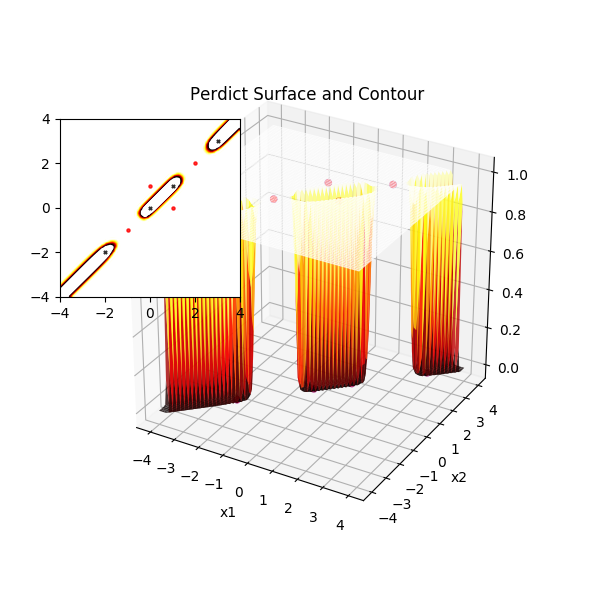
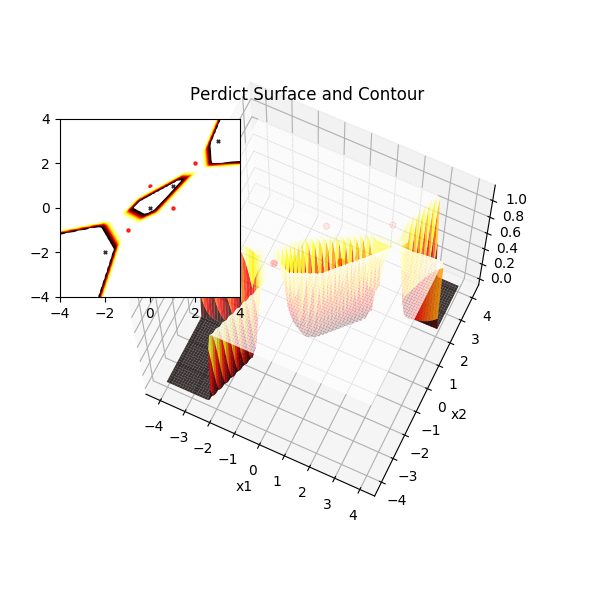
现在回归最根本的问题，尽管预测值和实际的标签已经完全一致，也即正确率 100%，那么神经网络是如何做到的呢？根据以往的线性分割模型无法分割 XOR 的点，直觉上可以想到，它可能进行了某种非线性分割，比如用一个椭圆（这里指高维曲面）把其中两个标签为 1 的点圈起来，外部则为 0 的点。但是如何验证推测呢？一个需要点发散思维的方式是绘图，这样就需要把图像限制在 3D 空间，也即特征变量最多有 2 个，XOR 训练集正好满足了这一特征，剩下的就是使用已经训练好的这组权重和偏置来对更多的假想特征值进行预测，来获取代价函数曲面。

  def draw_perdict_surface(self, X, y):
      from mpl_toolkits import mplot3d
      # XOR 特征值范围为 0-1，所以在 -2-2 区间作图足够反应整个预测平面
      x1 = np.linspace(-2, 2, 80, endpoint=True)
      x2 = np.linspace(-2, 2, 80, endpoint=True)

      title = 'Perdict Surface and Contour'
      # 生成网格化坐标
      x1, x2 = np.meshgrid(x1, x2)
      acts = np.zeros(x1.shape)
      for i in range(x1.shape[0]):
          for j in range(x1.shape[1]):# 计算输出层激活值
              acts[i,j] = self.feedforward(np.array([x1[i,j], x2[i,j]]).reshape(1,2))

      plt.figure(figsize=(6, 6))
      ax = plt.axes(projection='3d') # 绘制输出层激活值曲面图，透明度设置为 0.8 以便于观察样本点
      ax.plot_surface(x1, x2, acts, rstride=1, cstride=1, cmap='hot',
                      edgecolor='none', alpha=0.8)

      # 绘制样本点的输出层的激活值（蓝色）和标签值（红色）
      z = self.feedforward(X)
      ax.scatter3D(X[:,0], X[:,1], z, c='blue')
      ax.scatter3D(X[:,0], X[:,1], y[:,0], c='red')
      ax.set_title(title)
      ax.set_xlabel("x1")
      ax.set_ylabel("x2")
      # 绘制 3D 曲面的等高线
      ax0 = plt.axes([0.1, 0.5, 0.3, 0.3])
      ax0.contour(x1, x2, acts, 30, cmap='hot')
      plt.show()

实际上这里有些前提，例如输出层只有一个节点，我们可以直接使用输出值作为曲面的第三维，想象输出层有多个节点，那么其中一个节点的输出所能绘制的曲面就是高高低低，而低洼的地方对应样本点在该节点输出为 0 的特征，高凸的地方对应输出 1 的特征。

神经网络在 XOR 问题上的预测曲面（1）

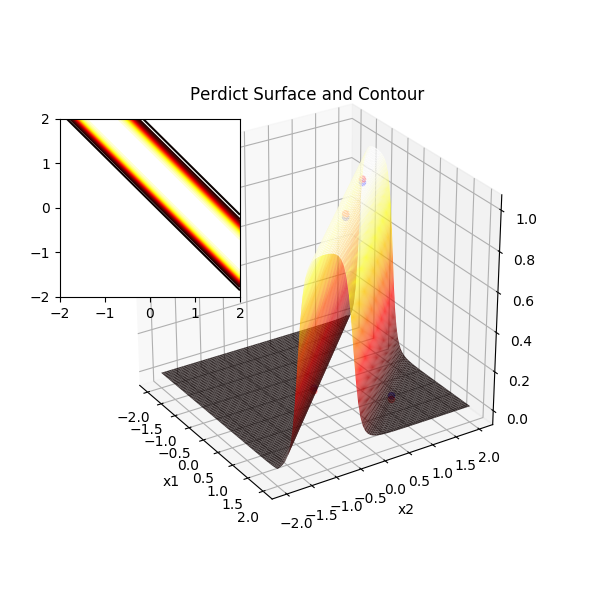
通过预测曲面图清楚地看到神经网络的强大之处，它非常聪明地生成了一对“翅膀”，靠近脊柱的地方凹陷，两侧翅膀高凸，观察样本点，预测值为1的样本点均落在了两侧翅膀上，预测值为 0 的样本点均落在了脊柱上。那么自然可以想到，另一种分割方法是预测值为1的样本点能落在脊柱上，而0的样本点落在翅膀上，此时脊柱隆起，而翅膀向下扇动：

神经网络在 XOR 问题上的预测曲面（2）

11.3.5. 梯度下降和交叉熵函数

在逻辑回归中，我们指出数据的标准化和权重的初始值异常重要，否则将导致求和函数的输出很大，继而使得 sigmoid 函数的输出接近 1 或者 -1，尽管正确的标签应该是 0 和 1（此时错误非常严重，预测和实际完全相反），此时的斜率非常小（曲线接近平行于 x 轴，导数很小），也就导致梯度下降在开始时非常缓慢。

神经网络也有如此问题，可以尝试将所有权重初始化为 3，偏置为 0，可以得到如下的下降曲线图，此时“学习效率”在初期非常低：

神经网络在权重比较大时初期下降速度变慢

我们观察神经网络在使用 MSE 代价函数时的权重调整计算公式，以理解为何会出现这类现象：

\[\delta^{(l)} = {{\mathbf{W}}^{(l)}}^T \delta^{(l+1)} \odot \frac {\partial {\phi (z^{(l)})}} {\partial {z^{(l)}}} \qquad (0)\]

\[\begin{eqnarray} \frac {\partial {J(w)}} {\partial {w^{(l-1)}_{ij}}} & = {a^{(l-1)}_j} \delta^{(l)}_i = \delta^{(l)} {a^{(l-1)}}^T \qquad (1) \end{eqnarray}\]

\[\frac {\partial {\phi (z^{(l)})}} {\partial {z^{(l)}}} = a^{(l)}_1(1-a^{(l)})\]

理论分析阶段已经指出，基于 MSE （二次代价函数）的代价函数时，公式(0) 的最后一层就需要乘以激活函数的导数部分（当权重较大时，斜率很小），这其实就是学习缓慢的原因所在。而交叉熵函数（最大对数似然函数）就不需要该项。可以想到如果去除该项，下降速度将加快，更改 mbatch_backprop 并不复杂：

  # 增加类型 type 参数，可以在 MSE 和交叉熵函数之间选择代价函数
  def mbatch_backprop(self, X, y, type='llh'):
      delta_b = [np.zeros(b.shape) for b in self.biases]
      delta_w = [np.zeros(w.shape) for w in self.weights]

      # feedforward
      if X.ndim == 1:
          X = X.reshape(1, X.ndim)
      if y.ndim == 1:
          y = y.reshape(1, y.ndim)

      activation = X.T
      acts = [activation] # list for all activations layer by layer
      zs = []             # z vectors layer by layer
      for b, W in zip(self.biases, self.weights):
          z = W.dot(activation) + b
          zs.append(z)
          activation = self.sigmoid(z)
          acts.append(activation)

      # 交叉熵函数时，第一项无需求乘以激活函数的导数，且无需取平均：样本数置为 1
      samples = X.shape[0]
      if type == 'llh':
          samples = 1
          delta = (acts[-1] - y.T) * self.sigmoid_derivative(zs[-1])
      else:
          delta = (acts[-1] - y.T) * self.sigmoid_derivative(zs[-1])
      delta_b[-1] = np.sum(delta, axis=1, keepdims=True)
      delta_w[-1] = np.dot(delta, acts[-2].transpose())
      for l in range(2, self.num_layers):
          sp = self.sigmoid_derivative(zs[-l])
          delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
          delta_b[-l] = np.sum(delta, axis=1, keepdims=True)
          delta_w[-l] = np.dot(delta, acts[-l-1].transpose())

      self.biases = [b-(self.eta) * nb / samples
                      for b, nb in zip(self.biases, delta_b)]
      self.weights = [w-(self.eta) * nw / samples
                      for w, nw in zip(self.weights, delta_w)]

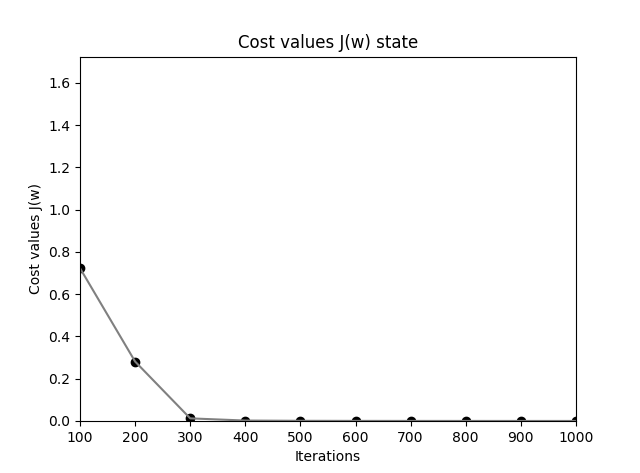
在同样的权重初始化下，可以看到使用交叉熵函数作为代价函数时，下降速度提高了 40 倍，以极快的速度下降到了指定的 tol 之下：

神经网络在使用交叉熵代价函数时下降速度加快

总结：使用 MSE 代价函数时，在神经元犯错严重的时候反而学习速率更慢。使用交叉熵代价函数时则神经元犯错严重时速度更快（最后一层的信号误差不再乘以激活函数的导数，只保留预测值和标签值差值，因为犯错严重，几乎相反，所以差值在最大值 1 或者 -1 附近）。特别指出，当使用次代价函数时，当神经元在接近正确的输出前只在少量样本犯了严重错误时，学习变得异常缓慢，使用交叉熵代价函数就可以缓解这种情况。

当然，如果我们把权重初始化得异常大，那么就会犯逻辑回归中的错误，误差值被钳制在了 1 和 -1 上，更大的错误并不能继续提高下降速度，所以对数据标准化以及权重随机初始在 0-1 之间是至关重要的。

另外要注意到我们这里只考虑了最后一层信号误差大小对梯度下降的影响，实际分析整个链式求导法则，可以发现每一层的误差都在不停减小，也即越靠近输入层，权重调整值越小，这是神经网络的另一大问题：梯度消失。

下面的数据源于随机初始化偏置，而权重调整为 0 时，进行一些周期的梯度下降后的权重和偏置值，明显发现后层的权重更大，前层权重更小：

weights: [array([[ 0.00099128,  0.00099128],
       [ 0.00130966,  0.00130966]]), array([[-0.14912941, -0.13739083]])]
biases: [array([[ 0.00759751],
       [-0.15077827]]), array([[ 0.13845597]])]

11.3.6. 柔性最大值 softmax

在二分类问题中输出层只有一个节点，使用 sigmoid 对数回归函数就可以很好地从概率上给与预测准确率的解释，但是在多分类问题上，各个节点激活值的和就完全可以大于 1，这样就无法满足概率解释的需求了。这里就引入了柔性最大值（softmax） 激活函数。后面的分析可以看到 softmax 激活函数：

• 不仅可以很好地从概率上解释预测的准确率；
• 同样它和 sigmoid 一样，可以解决使用交叉熵代价函数学习缓慢的问题。（显然我们不能为了解决一个问题而带来另一个问题，否则就不会引入 softmax了！）

柔性最大值只用于输出层，也即它为神经网络重新定义了输出层。在 softmax 激活值函数中，分母是经归一化处理的所有 K（输出层节点数）个线性函数之和，而分子为净输入 z，二者的比值即为特定样本属于第 j 个类别的概率：

\[\phi {(z^L_j)} = a^L_j = \frac {e^{z^L_j}}{\sum_k e^{z^L_k}} \qquad (0)\]

式中 L 表示输出层，j 表示输出层第 j 个节点，分母中的求和在所有的输出节点上进行，显然所有 K 个节点的激活输出的和总为 1，某个节点输出的增加将导致其他节点的输出降低，反之亦然。

\[\sum_j {a^L_j} = \frac {\sum_j e^{z^L_j}}{\sum_k e^{z^L_k}} = 1\]

另外注意到由于指数函数是正的，所以每个节点的激活输出总是正的，又由于它们的和总为1，柔性最大值在第 j 个节点上的输出可以被看做预测为分类 j 的似然概率。softmax 的实现非常简单：

  def softmax(self, z):
      return np.exp(z) / np.sum(np.exp(z), axis=0)

那么在使用柔性最大值激活函数时，代价函数如何表示呢？显然对于一个样本输入 x，对应一个 K 维的向量，其中有一个标签为 1，其余均为 0，我们的目标是使得对应标签 1 的输出（似然概率）最大即可：

\[L(w) = \prod_{i=1}^{n}P(y^i|x^i;w) = \prod_{i=1}^{n} {a^L_j}^i\]

其中 \({a^L_j}^i\) 表示输入样本 i 时，标签为 1 的节点 j 的输出。显然它对应的对数似然函数如下：

\[l(w) = \ln {(L(w))} = \sum_{i=1}^{n} \ln {{a^L_j}^i}\]

显然似然函数最大，则代价函数最小，加负号，并取平均，即可得到代价函数：

\[J(w) = -\frac {1}{n} \sum_{i=1}^{n} \ln {{a^L_j}^i}\]

只考虑一个样本时的代价函数：

\[j(w) = -\ln {a^L_j}\]

反向传播示意图

根据反向传播理论，一个权重的调整系数只与输入和输出信号误差有关，例如图中的 \(w^{(2)}_{11}\) 的调整系数只与 \(a^{(2)}_{1}\) 和 \(\delta^{(3)}_{1}\) 有关，其中：

\[\delta^{(3)}_{1} = \frac {\partial j(w)}{\partial z^{3}_1}\]

更普遍地，根据链式求导法则有：

\[\frac {\partial j(w)}{\partial z^{L}_i} = \frac {\partial j(w)}{\partial a^{L}_j} \frac {\partial a^{L}_j}{\partial z^{L}_i}\]

上式第 1 部分容易求得：

\[\frac {\partial j(w)}{\partial a^{L}_j} = -\frac{1} {a^{L}_j}\]

第 2 部分分为两种情况，当 i = j 时，表示当前节点的激活输出对当前节点的输入求偏导，i != j 时，表示对其他节点的输入求偏导，也即：

\[\begin{split}\frac {\partial a^{L}_j}{\partial z^{L}_i} = \left\{ \begin{array}{ll} a^{L}_j(1-a^{L}_j) & \textrm{$i=j$}\\ -a^{L}_j a^{L}_j & \textrm{$i!=j$}\\ \end{array} \right.\end{split}\]

将以上两部分合并后得到：

\[\begin{split}\frac {\partial j(w)}{\partial z^{L}_i} = \left\{ \begin{array}{ll} a^{L}_j - 1 & \textrm{$i=j$}\\ a^{L}_j & \textrm{$i!=j$}\\ \end{array} \right.\end{split}\]

观察上式，对于样本 i 的输入，由于 j 对应标签值为 1 的节点，其余节点标签值为 0，上式可以合并为：

\[\frac {\partial j(w)}{\partial z^{L}} = a^{L} - y^i\]

这和使用 sigmoid 激活函数的偏导是一致的，也即无需对反向传播的核心部分进行更改。再仔细观察这里的代价函数，与逻辑回归代价比较，显然当逻辑回归代价函数中所有标签为 0 的项都消去，它们就成了一样的形式。所以代价函数代码也无需更改。

这里只需要增加一个 softmax 开关，并更新前向传播的相关代码即可：

  def __init__(self, sizes, eta=0.001, epochs=1000, tol=None, alpha=0, softmax=True):
      ......
      # 根基 softmax 开关来设置不同的输出层激活函数
      self.outactive = self.sigmoid
      if softmax: self.outactive = self.softmax
      ......

  def feedforward(self, X):
      out = X.T
      for b, W in zip(self.biases[0:-1], self.weights[0:-1]):
          out = self.sigmoid(W.dot(out) + b)

      # 更新最后一层的激活值计算方式
      return self.outactive(self.weights[-1].dot(out) + self.biases[-1])

  def mbatch_backprop(self, X, y, type='llh', total=1):
      ......
      layers = 0
      for b, W in zip(self.biases, self.weights):
          z = W.dot(activation) + b
          zs.append(z)
          # 更新最后一层的激活值计算方式
          if layers == self.num_layers - 2:
              activation = self.outactive(z)
          else:
              activation = self.sigmoid(z)

          acts.append(activation)
          layers += 1

在 sklearn 中的 MLPClassifier 神经网络模块中，当遇到多分类情况时，输出层的激活函数默认设置为 softmax。本质上 softmax 不能带来任何性能的提升，只是方便从似然概率的角度对模型进行更好的解释。

11.3.7. 神经网络的强大表现力

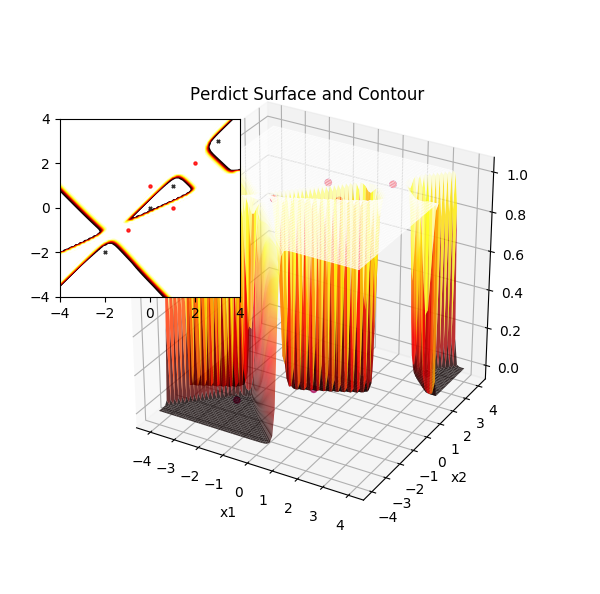
我们已经看到在 XOR 问题上神经网络预测曲面，它以非常具有弹性的方式扭曲，以适应不同样本所在的空间，并把它们包围或者分割开来。如果尝试在 XOR 数据的基础上，在 y = x 方向增加一些样本点，并且设置标签值互相交替，感性地看一下神经网络在“加强版” XOR 数据上的表现能力：

神经网络在交替数据上的强大表现能力

通过实践可以发现数据的分类交织越复杂，就要使用更多的隐藏节点，否则很难训练出有效的模型。这里使用 [2,10,1] 网络结构来训练样本，并观察上图中的等高线，负样本被一一限制在像蜂房一样的格子里，格子外则是正样本的领域。再观察 3D 图形，曲面在负样本聚集处快速下陷，形成一个蜂巢（或者抽屉，其实这里更像雪糕模型！）从而能把正负样本分离出来。

不要寄希望于每次训练都能得到这一组权重，让预测平面看起来如此完美无瑕，实际上 [2,10,1] 的网络参数已经达到了 (2*10 + 10) + (10*1 + 1) = 41 个（其中权重 2*10+10*1 =30 个，偏置 11 个），它能张成的空间早已超出人脑所能想象之外，上图只不过是数亿亿分之一的一个解决方案，大部分在训练集上的预测曲面可能是这样的： 它们长得奇形怪状，但是确实能够完美的分割训练集，但是对于未知数据的泛化能力就要大打问号了。

神经网络在交替数据上的一种不太好的分割

实际上上图已经出现了过拟合现象，神经网络如此强劲的表达能力能够将每一个样本点单独圈在一个蜂巢里，而让我们误以为它在训练集上正确率达到了百分之百，而实际上它的泛化能力可能差到了极致。

神经网络对随机点的分类边界投影

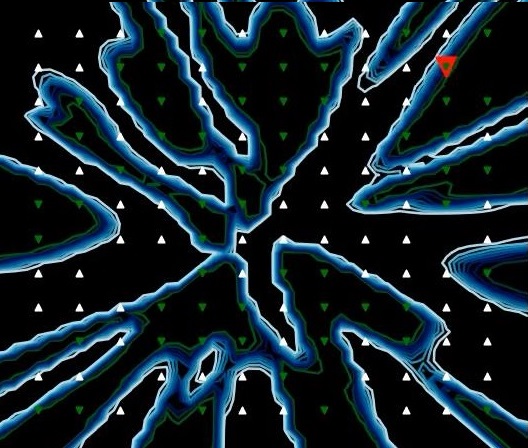
上图是对 12*12 个随机点组成的二分类 3D 曲面的投影，可以一睹神经网络强大的变形能力，不禁惊叹，神经网络似乎就是一个具有“思考”能力的超级可变函数，实际上在多样本多特征值的超级复杂网络上，它在高维空间变幻出各种分割子空间，我们根本不可能如此直观地观察边界投影，所以防止过拟合在神经网络模型上是非常重要的。

11.3.8. MNIST数据分类

这里使用 MNIST 数据集进行手写数字分类的测试，作为参照，使用 sklearn 的多层感知器 MLP 分类模型作为基准。

def sklearn_nn_test():
    from sklearn.neural_network import MLPClassifier
    images, labels, y_test, y_labels = dbload.load_mnist_vector(count=40000, test=10000)

    mlp = MLPClassifier(hidden_layer_sizes=(100,), max_iter=10000, activation='logistic',
                        solver='sgd', early_stopping=True, verbose=1, tol=1e-4, shuffle=True,
                        learning_rate_init=0.01)
    mlp.fit(images, labels)
    print("Training set score: %f" % mlp.score(images, labels))
    print("Test set score: %f" % mlp.score(y_test, y_labels))

该算法在迭代大约 30 次之后可以达到 96.5% 的测试集识别率，效果还是很好的：

Training set score: 0.999700
Test set score: 0.965000

def MNISTTrain():
    images, labels, y_test, y_labels = dbload.load_mnist_vector(count=40000, test=10000)

    y = np.zeros((labels.shape[0], 10))
    for i, j in enumerate(labels):
        y[i,j] = 1

    nn = NN([images.shape[1], 100, 10], eta=5, epochs=100000, tol=1e-4)
    nn.fit_mbgd(images, y, costtype='llh', batchn=256, x_labels=labels,
                Y_test=y_test, y_labels=y_labels)

这里对 fit_mbgd 函数增加一些用于在训练过程中用到的评估参数，并新增了评估函数：

  def evaluate(self, x_train, x_labels, y_test, y_labels):
      pred = self.predict(x_train)
      error = pred - x_labels
      error_entries = np.count_nonzero(error != 0)

      test_entries = x_labels.shape[0]
      print("Accuracy rate {:.02f}% on trainset {}".format(
            (test_entries - error_entries) / test_entries * 100,
            test_entries), flush=True)

      pred = self.predict(y_test)
      error = pred - y_labels
      error_entries = np.count_nonzero(error != 0)

      test_entries = y_labels.shape[0]
      print("Accuracy rate {:.02f}% on testset {}".format(
            (test_entries - error_entries) / test_entries * 100,
            test_entries), flush=True)

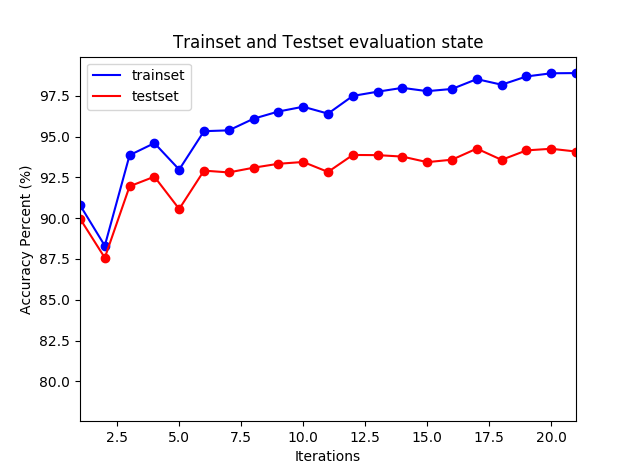
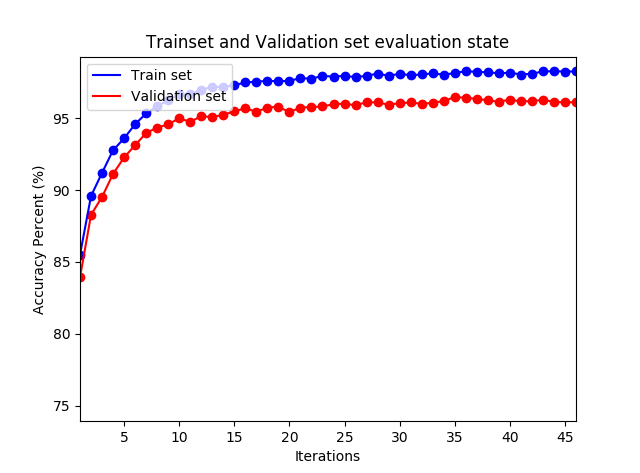
在 fit_mbgd 中每次统计代价值时，均对训练集和测试集进行评估，以观察神经网络的学习进度。注意这里的学习率 5 是经过多次实验验证的，它是训练时间和良好的结果的权衡的结果，较大的学习率有助于跳出局部最小值。在迭代大约 10 多次后，测试集的正确率达到了 94%，之后尽管训练集的正确率还在上升，但是测试集的准确率基本不动了。

Accuracy rate 99.72% on trainset 40000
Accuracy rate 94.60% on testset 10000

MNIST 训练集和测试集分类准确率曲线图

实际上神经网络在 8 个迭代期后的学习已经基本无效了，它无法泛化到测试数据上。所以这不是有效的学习。神经网络在这个迭代期后就过度拟合（overfitting）或者过度训练（overtraining）了。

检测过度拟合的明显方法就是跟踪测试数据集合上的准确率随训练变化情况。如果测试数据上的准确率不再提升，那么就应该停止训练。要么换一组随机权重参数，要么调整学习率或者其他超参数。所以通常把训练数据集分成两部分：训练数据集和校验数据集，校验数据集用于预防过度拟合。

11.3.9. 交叉验证

现实中，在实际解决问题时，人们总是要进行各种权衡，也即没有一击必中的解决方案。所以是选用几种不同的算法来训练模型，并比较它们的性能，从中选择最优的一个是惯常的做法。但是评估不同模型的性能优劣，需要确定一些衡量标准。常用的标准之一就是分类的准确率，也即被正确分类的样例所占的比例。这种方法被称为交叉验证：将训练数据集划分为训练集和校验集，从而对模型的泛化能力进行评估。

交叉验证（CV，Cross Validation）法又分为两种：Holdout 交叉验证（Holdout cross-validation）和 K 折交叉验证（K-fold cross-validation）。

Holdout 留出法，MNIST 分类示例中将初始数据集（initial dataset）分为训练集（training dataset）和测试集（test dataset）两部分，就是一种 Holdout 方法。训练集用于模型的训练，测试集进行性能的评价。然而从上述训练过程可以看到，在实际操作中，常常需要反复调试和比较不同的参数以提高模型在新数据集上的预测性能。这一调参优化的过程就被称为模型的选择（model selection），这是在给定分类问题上调整参数以寻求最优值（也称为超参，hyperparameter，通常指权重系数之外的参数，例如学习率）的过程。

在这一过程中如果重复使用同样的测试集，测试集等于成了训练集的一部分，此时模型容易发生过拟合，也即模型最终将能很好的泛化到训练集和测试集，但是在新数据上表现糟糕。

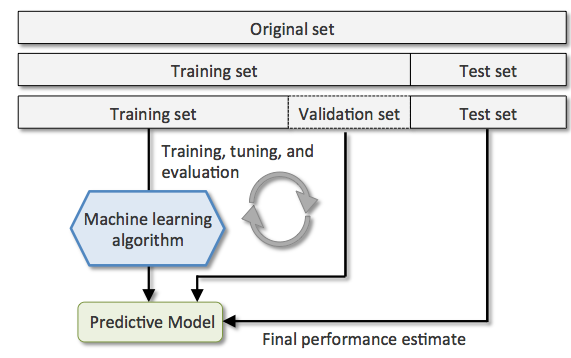
所以改进的 Holdout 方法将数据集分成 3 部分：

• 训练集（training set），训练集用于不同算法模型的训练。
• 验证集（validation set），模型在验证集上的性能表现作为模型选择的标准。
• 测试集（test set）用于评估模型应用于新数据上的泛化能力。

使用模型训练及模型选择阶段不曾使用的新数据作为测试集的优势在于：评估模型应用于新数据上能够获得较小偏差（防止过拟合）。

Holdout 交叉验证模型（图来自 Python Machine Learning）

Holdout 方法的缺点在于性能的评估对训练集和验证集分割方法（例如分割比例）是敏感的。

我们必须确定训练退出的标准，而这是非常困难的，最简单的方式就是评估验证集的分类准确度的变化，如果最近几个迭代周期的准确度变化很微弱，那么就可以停止训练了。

实际上我们很快就会发现，分类准确率和训练集和验证集分割比例呈正相关，也即训练集越大，验证集准确率越高，与此同时训练集的准确率也越高，也即扩大训练数据集可以防止模型的过拟合，但是实际中收集更多数据是非常昂贵的，甚至是不现实的。

Holdout 方法提供了一种观察算法拟合情况的视窗，它揭示出数据集的独立同分布特征，如果算法能够很好地学习到真实数据的特征，那么它在这三个数据集上的得分就应该是基本一致的，而不是在训练集上很高，而在其他测试集上效果很一般。

Holdout 常用于寻找理想的超参数，以取得三个数据集上的平衡（既不欠拟合也不过拟合）。K 折交叉验证是对Holdout 方法的扩展，它具有更实际的应用意义。

11.3.10. K 折交叉验证

K-折交叉验证（K-fold Cross Validation，K-CV） 随机将训练数据集划分（通常为均为划分）为 K 个子集，其中 K-1 个用于模型的训练，剩余的 1 个用于测试。依次使用第 1 到 K 个子集用于测试，重复此过程 K 次，就得到了 K 个模型及对模型性能的评价。

K-CV方法的优势在于（每次迭代过程中）每个样本点只有一次被划入训练数据集或测试数据集的机会，与 Holdout方法相比，这将使得模型性能的评估具有较小的方差（防止了过拟合）。

K 的标准值为 10，这对大多数应用来说都是合理的。但是，如果训练数据集相对较小，那就有必要加大 K 的值。如果增大 K 的值，在每次迭代中将会有更多的数据用于模型的训练，这样通过计算各性能评估结果的平均值对模型的泛化性能进行评价时，可以得到较小的偏差（防止了欠拟合）。当然 K 值取得较大，处理时间也随之增加。

通常情况下，我们将K-CV 方法用于模型的调优，也就是找到使得模型泛化性能最优的超参值。一旦找到了满意的超参值，就在全部的训练集上重新训练模型，并使用独立的测试数据集对模型性能做出最终评价。

sklearn 实现了 KFold 算法，示例代码如下：

def kfold_estimate(k=10):
    from sklearn.model_selection import KFold
    images, labels, y_test, y_labels = dbload.load_mnist_vector(count=500, test=100)

    scores_train = []
    scores_validate = []
    scores_test = []
    cv = KFold(n_splits=k, random_state=1)
    for train, test in cv.split(images, labels):
        X_images, X_labels = images[train], labels[train]
        y = np.zeros((X_labels.shape[0], 10))
        for i, j in enumerate(X_labels):
            y[i,j] = 1

        nn = NN([X_images.shape[1], 100, 10], eta=1, epochs=10000, tol=1e-2)
        nn.fit_mbgd(X_images, y, costtype='llh', batchn=64)

        # 分别在训练集，交叉验证集和测试集上验证第 k 次的得分
        score = heldout_score(nn, X_images, X_labels)
        test_entries = X_labels.shape[0]
        print("Accuracy rate {:.02f}% on trainset {}".format(
              score, test_entries), flush=True)
        scores_train.append(score)

        score = heldout_score(nn, images[test], labels[test])
        test_entries = labels[test].shape[0]
        print("Accuracy rate {:.02f}% on vcset {}".format(
              score, test_entries), flush=True)
        scores_validate.append(score)

        score = heldout_score(nn, y_test, y_labels)
        test_entries = y_test.shape[0]
        print("Accuracy rate {:.02f}% on testset {}".format(
              score, test_entries), flush=True)
        scores_test.append(score)

    print(scores_train)
    print(scores_validate)
    print(scores_test)

如果测试样本的分类是不均衡的，就应该使用分层 K 折交叉验证，它对标准 K 折交叉验证做了稍许改进，可以获得偏差和方差都较低的评估结果，特别是类别比例相差较大时。在分层交叉验证中，类别比例在每个分块中得以保持，这使得每个分块中的类别比例与训练数据集的整体比例一致。对应的实现为 sklearn 中的 StratifiedKFold 类：

# 初始化分层 K 折交叉验证类对象
from sklearn.model_selection import StratifiedKFold
cv = StratifiedKFold(n_splits=k, random_state=1)

实际上 MNIST 训练数据集的分类就不是均分的：

images, labels, y_test, y_labels = dbload.load_mnist_vector(count=40000, test=10000)

unique = np.unique(labels)
for i in unique:
    print(i, ':\t', np.sum(labels==i))

>>>
0 :      3924
1 :      4563
2 :      3943
3 :      4081
4 :      3909
5 :      3604
6 :      3975
7 :      4125
8 :      3860
9 :      4016

K 折交叉验证的一个特例是留一（Leave-one-out，LOO-CV）交叉验证法。如果设原始数据有 N 个样本，那么LOO-CV 就是 N-CV，即每个样本单独作为验证集，其余的 N-1 个样本作为训练集，所以 LOO-CV 会得到 N 个学习模型，用这 N 个模型最终的验证集的分类准确率的平均数作为此 LOO-CV 分类器的性能指标。相比于前面的 K-CV，LOO-CV有两个明显的优点：

• 每一回合中几乎所有的样本皆用于训练模型，因此最接近原始样本的分布，这样评估所得的结果比较可靠。
• 实验过程中没有随机因素会影响实验数据，确保实验过程是可以被复制的。

但 LOO-CV 的缺点是计算成本高，需要建立的模型数量与原始数据样本数量相同，当原始数据样本数量相当多时，LOO-CV 在实作上便有困难，除非每次训练分类器得到模型的速度很快，或是可以用并行化计算减少计算所需的时间。

使用不同的分类模型进行 K 折交叉验证，如果平均得分比较高，方差比较低，那么这个模型的泛化能力就较强，且性能稳定。

11.3.11. 梯度检验

神经网络是一个较为复杂的模型，当使用梯度下降算法时，可能存在一些不易察觉的错误，这意味着，虽然代价看上去在不断减小，但最终的结果可能并不是最优解。为了避免这样的问题，我们采取一种叫做数值梯度检验（Numerical Gradient Checking）的方法来发现问题。

这种方法的思想是通过估计梯度值来检验计算的导数值是正确。对梯度的估计采用在代价函数上沿着切线的方向选择离两个非常近的点然后计算两个点的平均值用以估计梯度。只针对一个权重参数的检验公式为：

\[\frac {\partial {J(w)}} {\partial {w_i}} = \frac {J(w_1,w_2 \cdots w_i+\epsilon \cdots w_n) - J(w_1,w_2 \cdots w_i-\epsilon \cdots w_n)} {2\epsilon}\]

然后可以设定所有权重均为值 1，然后使用上式分别计算出所有的权重值然后和反向传播计算出的偏导值比较，如果偏差很大则说明代价函数或者反向传播算法实现有问题。当然也可以多设定几组初始值以进行多重验证。

这里需要对反向传播函数做一些调整，例如返回调整的 delta 值：

  def mbatch_backprop(self, X, y, type='llh'):
      delta_b = [np.zeros(b.shape) for b in self.biases]
      delta_w = [np.zeros(w.shape) for w in self.weights]
      ......

      # backpropagation
      samples = X.shape[0]
      if type == 'llh':
          delta = (acts[-1] - y.T)
      else:
          delta = (acts[-1] - y.T) * self.sigmoid_derivative(zs[-1])
      delta_b[-1] = np.sum(delta, axis=1, keepdims=True)
      delta_w[-1] = np.dot(delta, acts[-2].transpose())
      for l in range(2, self.num_layers):
          sp = self.sigmoid_derivative(zs[-l])
          delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
          delta_b[-l] = np.sum(delta, axis=1, keepdims=True)
          delta_w[-l] = np.dot(delta, acts[-l-1].transpose())

      ......
      # 返回 delta 值
      for i in range(len(delta_b)):
          delta_b[i] /= samples
      for i in range(len(delta_w)):
          delta_w[i] /= samples
      return delta_b, delta_w

  # MSE 代价函数
  def quadratic_cost(self, X, y):
      return np.sum((self.feedforward(X) - y.T)**2) / y.shape[0] / 2

  # 对数最大似然代价函数
  def loglikelihood_cost(self, X, y):
      output = self.feedforward(X)

      diff = 1.0 - output
      diff[diff <= 0] = 1e-15
      return np.sum(-y.T * np.log(output) - ((1 - y.T) * np.log(diff))) / y.shape[0]

gd_checking 函数用于梯度校验，整个流程都是很清晰的，首先通过以上公式来评估偏导数，然后通过反向传播计算偏导数，计算差值来观察算法是否正确。

  # 校验函数，costtype 指定代价函数，llh 表示最大似然函数
  def gd_checking(self, X, y, costtype='llh'):
      # init all weights as 1
      self.biases = [np.ones((l, 1)) for l in self.sizes[1:]]
      self.weights = [np.ones((l, x)) for x, l in zip(self.sizes[:-1], self.sizes[1:])]
      epsilon = 1e-4

      costfunc = self.quadratic_cost
      if costtype == 'llh':
          costfunc = self.loglikelihood_cost

      # 使用公式计算偏导数
      partial_biases = [np.zeros((l, 1)) for l in self.sizes[1:]]
      for i in range(len(self.biases)):
          for j in range(self.biases[i].size):
              self.biases[i][j] += epsilon
              plus = costfunc(X,y)
              self.biases[i][j] -= 2*epsilon
              minus = costfunc(X,y)
              self.biases[i][j] += epsilon
              partial_biases[i][j] = ((plus - minus)/ 2 / epsilon)

      partial_weights = [np.zeros((l, x)) for x, l in zip(self.sizes[:-1], self.sizes[1:])]
      for i in range(len(self.weights)):
          for j in range(self.weights[i].shape[0]):
              for k in range(self.weights[i].shape[1]):
                  self.weights[i][j,k] += epsilon
                  plus = costfunc(X,y)
                  self.weights[i][j,k] -= 2*epsilon
                  minus = costfunc(X,y)
                  self.weights[i][j,k] += epsilon
                  partial_weights[i][j,k] = ((plus - minus)/ 2 / epsilon)

      # 使用后向传播计算偏导数
      delta_b, delta_w = self.mbatch_backprop(X,y, type=costtype, total=X.shape[0])

      # 计算差值，应该很小
      diff_bs = [b - nb for b, nb in zip(partial_biases, delta_b)]
      diff_ws = [w - nw for w, nw in zip(partial_weights, delta_w)]

      print(diff_bs)
      print(diff_ws)

11.3.12. L2正则化

正则化可以有效防止模型的过拟合。神经网络同样可以使用正则化技术来缓解过度拟合。正则化的交叉熵代价函数公式：

\[J(w) = -\frac{1}{n}\biggl[\sum_{i=1}^{n}\sum_{k=1}^{K}y^i_k {\ln {(\phi (z^i))}}_k + (1-y^i_k) {\ln {(1-\phi (z^i))}}_k \biggr]+ \frac{\lambda}{2n} \sum_{w}w^2\]

其中的 λ > 0，被称为正则化参数，值越大，正则化对权重的收缩越强，规范化项不包含偏置项。

同样对于 MSE 形式的二次代价函数，正则化形式如下：

\[J(w) = \frac{1}{2n}\sum_{i=1}^{n}\sum_{k=1}^{K}({\hat y}^i_k - {y^i_k})^2 + \frac{\lambda}{2n} \sum_{w}w^2\]

在线性回归中已经知道 λ 参数大小决定了权重系数的收缩程度。规范化让神经网络倾向于寻找较小的权重来最小化代价函数。λ 越小，就倾向于原始代价函数，反之，倾向于小的权重。

显然以上两公式增加的正则化项是相同的，所以对于偏导数来说增加项也是相同的：

\[\begin{split}\begin{eqnarray} J(w) & = & J(w)_0 + \frac{\lambda}{2n} \sum_{w}w^2 \\ \frac {\partial {J(w)}} {\partial {w}} & = & \frac {\partial {J(w)_0}{w}}{\partial w} + \frac {\lambda}{n}{w} \\ \Delta_w & = & \eta(\frac {\partial {J(w)_0}}{\partial w} + \frac {\lambda}{n}w) \end{eqnarray}\end{split}\]

所以可以得到：

\[w - \Delta_w = w - \eta(\frac {\partial {J(w)_0}}{\partial w} + \frac {\lambda}{n}w) = (1- \frac {\eta \lambda}{n})w - \eta \frac {\partial {J(w)_0}}{\partial w}\]

我们增加 alpha 表示正则化参数，并更新初始化函数，梯度下降函数和代价函数：

  def __init__(self, sizes, eta=0.001, epochs=1000, tol=None, alpha=0):
      ......
      self.alpha = alpha # for regulization
      ......

  def mbatch_backprop(self, X, y, type='llh', total=1):
      ......
      # 只需调整 weights 项，正则化不影响偏置项，total 表示所有样本数
        self.weights = [(1-self.eta*self.alpha/total)*w - self.eta * nw
                        for w, nw in zip(self.weights, delta_w)]
      ......

  # 增加正则化项的代价计算函数
  def regulization_cost(self, X, y):
      return 0.5 * (self.alpha / y.shape[0]) * \
             sum(np.linalg.norm(w)**2 for w in self.weights)

  def quadratic_cost(self, X, y):
      cost = np.sum((self.feedforward(X) - y.T)**2) / y.shape[0] / 2
      if self.alpha:
          cost += self.regulization_cost(X,y)
      return cost

  def loglikelihood_cost(self, X, y):
      output = self.feedforward(X)

      diff = 1.0 - output
      diff[diff <= 0] = 1e-15
      cost = np.sum(-y.T * np.log(output) - ((1 - y.T) * np.log(diff))) / y.shape[0]

      if self.alpha:
          cost += self.regulization_cost(X,y)
      return cost

更新测试函数，使用以下参数进行模型训练，经过多次尝试，发现 alpha 取 15 效果较好。

def MNISTTrain():
    import crossvalid
    images, labels, y_test, y_labels = dbload.load_mnist_vector(count=40000, test=10000)
    X_images, validate, X_labels, validate_labels = \
        crossvalid.data_split(images, labels, ratio=0.1, random_state=None)

    y = np.zeros((X_labels.shape[0], 10))
    for i, j in enumerate(X_labels):
        y[i,j] = 1

    nn = NN([X_images.shape[1], 100, 10], eta=1, epochs=100000, tol=1e-6, alpha=15)
    nn.fit_mbgd(X_images, y, costtype='llh', batchn=256, x_labels=X_labels,
                y_test=validate, y_labels=validate_labels)

    pred = nn.predict(y_test)
    error = pred - y_labels
    error_entries = np.count_nonzero(error != 0)

    test_entries = y_test.shape[0]
    print("Accuracy rate {:.02f}% on trainset {}".format(
          (test_entries - error_entries) / test_entries * 100,
          test_entries), flush=True)

MNISTTrain()

>>>
Accuracy rate 98.26% on trainset 36000
Accuracy rate 96.12% on testset 4000
Accuracy rate 96.50% on trainset 10000

显然对比正则化前的 94.60%，在测试集上正则化后提升了 1.9 个百分点，效果是非常明显的。此时的训练集并没有达到 99% 以上的准确率，却得到了更好的泛化效果。

正则化后的测试集和验证集正确率曲线图

为了寻找比较合适的 alpha 参数，可以尝试绘制 alpha 和测试集准确率的关系曲线图。

实践证明，由于正则化项的存在，形成对权重大小的钳制，所以在使用不同随机权重值时，效果更加稳定，很容易复现出同样的结果。如果代价函数未规范化，那么某些权重度可能不停增加，有些会不停减小，随着时间的推移，这会导致大权重的调整比例越来越小，从而下降越来越慢。

11.3.13. 梯度消失问题

目前为止我们只使用了单个隐藏层的神经网络。如果我们尝试增加层数，出乎意料的是并没有因为层数的增加而带来明显的分类正确率的提高。

我们已经指出交叉熵函数可以缓解最后一层权重调整缓慢的问题，但是分析整个链式求导法则，可以发现每前一层的调整值都在不停减小，也即越靠近输入层，权重调整值越小。

不同层偏置调整大小对比

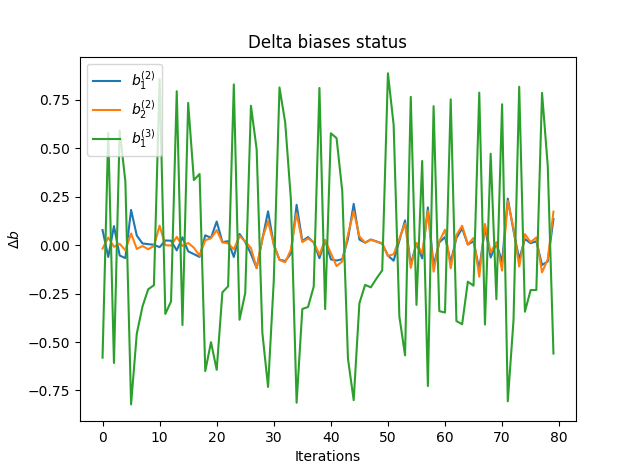
上图是在使用[2,2,1]神经网路拟合 XOR 数据时，记录了迭代 100 次时第 2 层和第 3 层偏置项的调整大小，显然第 3 层的调整量整体是第 2 层 3-4 倍。这不是偶然的，因为链式法则使得前一层总要在后一层的基础上乘以 sigmoid 关于 z 的偏导数，显然该值最大只有 0.25，这和我们的观察倍数相符。各层权重项的调整值和偏置项具有相同规律，并且由于输入部分最大只能接近 1 所以调整更小。

\[\delta^{(l)} = {{\mathbf{W}}^{(l)}}^T \delta^{(l+1)} \odot \frac {\partial {\phi (z^{(l)})}} {\partial {z^{(l)}}} \qquad (0)\]

\[\begin{eqnarray} \frac {\partial {J(w)}} {\partial {w^{(l-1)}_{ij}}} & = {a^{(l-1)}_j} \delta^{(l)}_i = \delta^{(l)} {a^{(l-1)}}^T \qquad (1) \end{eqnarray}\]

这个现象被称作是梯度消失问题（vanishing gradient problem）。可以想象如果链式中的 w 项大于 4，那么 w 可以中和导数带来的缩小，但是这又会导致梯度激增问题（exploding gradient problem）。实际上遇到梯度消失问题要远远大于梯度激增，因为过大的 w 会让加权和 z 比较大，从而导致偏导数很小，以至于逼近0，所以乘积就会小于 1。

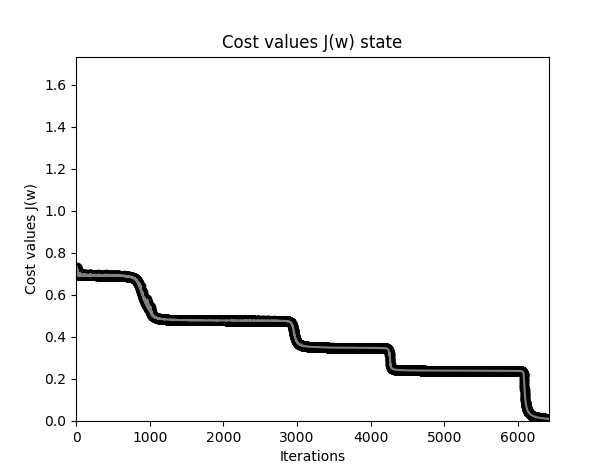
一种尝试解决梯度消失的办法是给与不同层以不同的学习率，前层总比后一层学习率大一些，比如大 2-4 倍，但是当层数比较多时，相当于增加了非常多的超参数，所以通常由程序自动适配学习率。实际上多层神经网络的学习率不能设置得太大，且下降函数具有明显阶梯特征：

具有三个隐藏层神经网络下降曲线

另外一种方法是中间层的激活函数使用 ReLU (修正线性单元)，也即 f(z)=max(0,z)，显然它的导数只有 0 和 1：

• 提高 ReLU 的带权输入不会导致其饱和，所以就不存在梯度下降问题。
• ReLU 的计算比 sigmoid 激活函数计算简单，没有指数运算，程序执行更快。
• 但是，当带权输入是负数时，梯度就消失了，神经元就完全停止了学习。此时可以使用改良版的 ELU 或者 LReLU 来代替 ReLU。
• 由于图片像素值均是大于 0 的，所以在加权之后的和也是倾向于大于 0 的，此时使用 ReLU 负数梯度消失问题对图片分类影响就不大了，在使用 ReLU 时可以进行归一化，但是不要进行标准化。

ReLU 在 0 点不可导，意味着它在0点有无数条切线，而梯度下降是沿着切线反方向进行的，所以只要从 [0, 1] 取值均是可以的，通常取 0 值。

sigmoid 激活函数预测曲面图

relu 激活函数预测曲面图

尽管 ReLU 在图片分类上有长足之处，但是理论上还没有一个关于什么时候什么原因导致 ReLU 表现更好的深度的理解。以上两幅图均是对加强版的异或问题进行分类，采用同样的单隐藏层 10 节点神经网络模型。从直观上看它们的边界一个趋向于圆弧形，一个趋向于折线形，从直觉上也可以感受到为何会有如此形状：尽管我们使用层叠方式通过线性和非线性叠加了无数的 sigmoid 和 ReLU 变换，它们在最终的输出上总是会反映出神经网络变换函数的本质，否则变换代价函数将不能带来任何预测性能的改变。

显然我们不能武断地说明哪一种模型更好，这显然和数据的分布有关。现实世界中抽屉，蜂巢似乎更倾向于使用折线形状，也许这就是 ReLU 在虚拟的高维空间对二进制数据隔离更好的原因，毕竟二进制数据也是对现实世界的反映， 当然这种基于假想的推测确实牵强。实际中还是要进行效果对比才能针对目标任务做出更好的代价函数选择。

def sklearn_nn_test():
    from sklearn.neural_network import MLPClassifier
    images, labels, y_test, y_labels = dbload.load_mnist_vector(count=40000, test=10000)

    mlp = MLPClassifier(hidden_layer_sizes=(100,), max_iter=10000, activation='relu',
                        solver='sgd', early_stopping=False, verbose=1, tol=1e-6, shuffle=True,
                        learning_rate_init=0.01, alpha=0.5)

    mlp.fit(images, labels)
    print("Training set score: %f" % mlp.score(images, labels))
    print("Test set score: %f" % mlp.score(y_test, y_labels))

sklearn_nn_test()

>>>
Training set score: 0.990325
Test set score: 0.974300

使用 sklearn 中的 MLPClassifier 模型，激活函数更改为 relu 方式，在 MNIST 的测试数据集上取得了 97.43% 的成绩。

11.3.14. 基于Pipline的工作流

通常机器学习有着一样的流程：数据处理（数据转换，标准化等），模型拟合，模型评估，参数调优等步骤。scikit-learn 中的 Pipline 类可以创建包含任意多个处理步骤的模型，并将模型用于新数据的预测。

Pipeline对象采用元组的序列作为输入，其中每个元组中的第一个值为一个字符串，它可以是任意的标识符，我们通过它来访问管线中的元素，而元组的第二个值则为scikit-learn中的一个转换器（transforms，需要实现 fit 和 transform 方法）或者评估器（estimator，只需实现 fit 方法），管线中可以安排多种处理工序，最后一道工序通常是评估器。

from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
pipe = Pipeline([('scl', StandardScaler()),
                 ('lr', LinearRegression(fit_intercept=True))])
X = np.linspace(1,11,10).reshape(10,1)
y = X * 2 + 1
pipe.fit(X, y)
print(pipe.predict([[1],[2]]))

>>>
[[ 3.]
 [ 5.]]

以上示例，首先创建一条管线，管线元组序列包含数据标准化部分和回归拟合部分，通过管线对象 pipe 可以直接进行拟合和预测。

11.3.15. 学习曲线和验证曲线

通常使用代价函数的下降曲线来评估学习率的设定，太大不容易收敛，太小下降速度太慢。当选定较好的学习率后，通常测试不同数量级的正则化参数，选定理想的正则化参数后，再反过来调整学习率。

可以通过观察校验集的得分来决定迭代是否停止，然而实际上对于深层网络来说，可能会出现梯度暂停下降现象，此时的得分也不再上升，所以武断地选择停止可能不是一个好主意。

是否有统一的一套流程来针对各类超参数进行筛选，并对模型性能进行评估呢。一个强大的工具就是学习曲线和验证曲线：

• 学习曲线用来判定学习是否过拟合（高方差，High variance）或欠拟合（高偏差，High bias）。
• 验证曲线，可以帮助寻找学习算法中的各类问题点。

通常一个模型的构造越复杂（比如神经元节点数，层数；多项式的次数），参数越多那么这个模型的容量就越大，学习能力就越强，就像一个水库，水库越深，面积越大那么它的容积也就越大。显然对于复杂模型，在有限的训练数据集下，很容易出现过拟合，也即可以百分百地对训练集数据正确分类，但是对于未知数据的泛化能力却很差。通常情况下，收集更多的训练样本有助于降低模型的过拟合程度。但是收集更多数据成本高昂，或者根本不可行（理由有些罕见疾病的数据很难收集）。

通过将模型的训练及准确性验证看作是训练数据集大小的函数，并绘制图像，可以很容易得出模型是面临高方差还是高偏差的问题，以及收集更多的数据是否有助于解决问题。

def sklearn_mnist(ratio=1.0, hidden_neurons=10, alpha=0):
    from sklearn.neural_network import MLPClassifier
    images, labels, y_test, y_labels = dbload.load_mnist_vector(
            count=int(40000 * ratio), test=int(10000 * ratio))

    mlp = MLPClassifier(hidden_layer_sizes=(hidden_neurons,), max_iter=10000,
                        activation='relu',solver='adam', early_stopping=False,
                        verbose=1, tol=1e-6, shuffle=True,
                        learning_rate_init=0.01, alpha=alpha)

    mlp.fit(images, labels)
    return mlp.score(images, labels), mlp.score(y_test, y_labels)

sklearn_mnist 针对 MNIST 数据集进行训练，可以设定训练集和测试集的数据比例，hidden_neurons 则用于设置隐藏层的节点数，越大神经网络容量就越大，越容易过拟合。relu 和 adam (或 lbfgs，一种梯度下降加速算法，适用于小型数据集，adam 适用于更大型数据集)可以加速训练。

def plot_learning_curve():
    train_scores,test_scores,percents = [],[],[]
    for i in np.linspace(1, 10, 50, endpoint=True):
        train_score, test_score = sklearn_mnist(i * 0.1)
        print("Training set score: %f" % train_score)
        print("Test set score: %f" % test_score)
        train_scores.append(train_score)
        test_scores.append(test_score)
        percents.append(i*0.1*40000)

    plt.figure()
    plt.title("Train and Test scores status")
    plt.xlabel("Trainset samples")
    plt.ylabel("Scores (%)")

    plt.plot(percents, train_scores, label='Train Scores', c='black')
    plt.plot(percents, test_scores, label='Test Scores', c='gray')
    plt.scatter(percents, train_scores, c='black')
    plt.scatter(percents, test_scores, c='gray')

    # target horizontal line
    plt.hlines(0.97, 0, 40000, alpha=0.5, linestyle='--')
    plt.legend(loc='upper right')
    plt.show()

MNIST 数据集在单层 10 隐藏节点神经网络下的准确率曲线

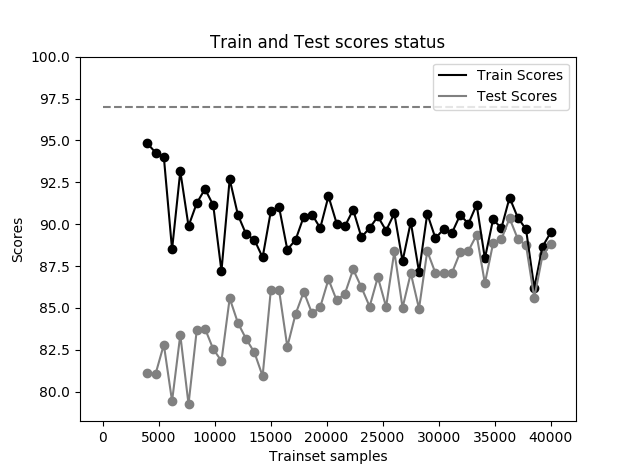
上图是针对 MNIST 数据集的准确率曲线，分别在 40000 个训练集上按比例训练了 50 次，也即每次取训练集数分别为 1/50，2/50，测试集按同样比例选取。图中的水平虚线是假想的目标准确率，实际上目标准确率是未知的，只是建立在许多模型的多次实验中得出的，这里用来作为参考。可以发现：

• 训练集越小，在训练集上的得分越高，越容易过拟合，随着训练集的增大，由于单层 10 隐藏节点神经网络容量有限，能够学到的特征越来越少，导致训练集上的得分越来越低。
• 当训练集很小时，模型没有学习到足够的特征，导致测试集得分一开始很低，随着训练数据集的增大，网络学到了更多特征，测试集得分慢慢上升，直至训练数据集扩充到所有训练数据，此时模型的训练准确率和测试集的准确率都很低，这表明此模型未能很好地拟合数据。

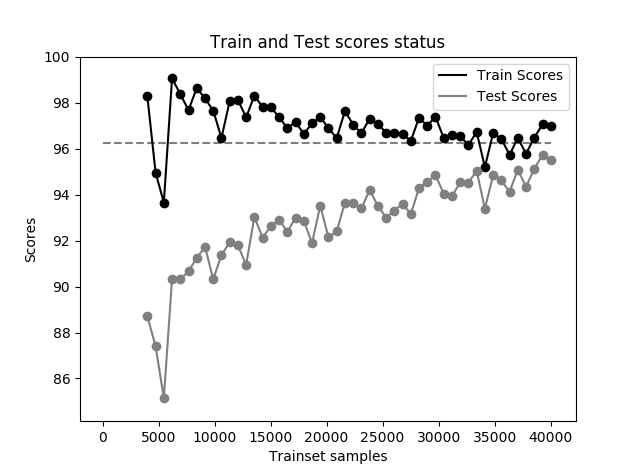
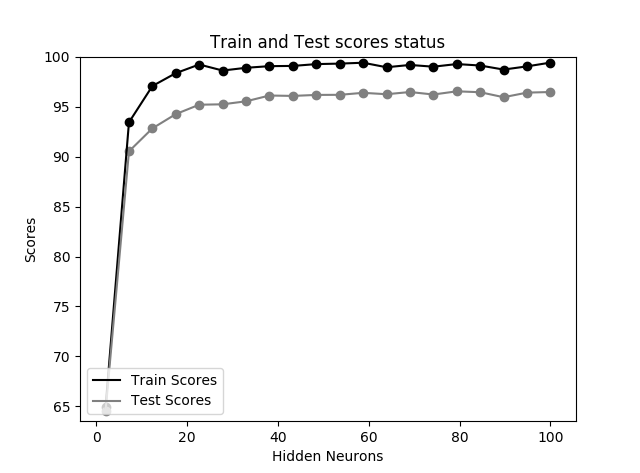
我们尝试将隐藏神经节点从 10 个扩充到 100 个，此时模型不再欠拟合，而是更容易过拟合。

MNIST 数据集在单层 100 隐藏节点神经网络准确率曲线

观察上图，当训练集非常大时，依然可以达到 98% 左右的准确率，而测试集只能徘徊在 95% 左右而不再上升，训练集准确率和测试集准确率有着一段差距，进入了过拟合状态。

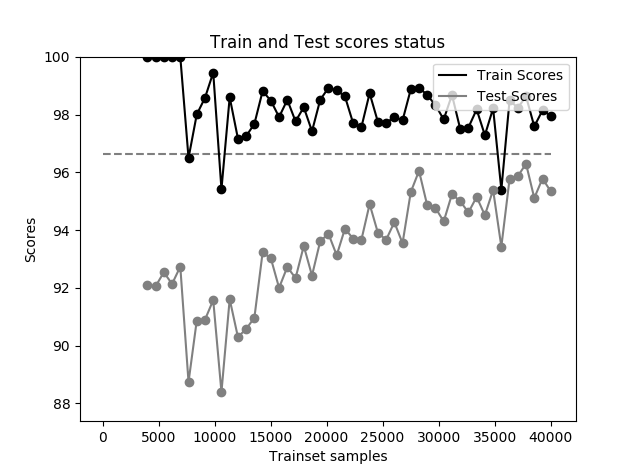
此时将 alpha 调整为 0.1，也即增加正则化项，以防止过拟合，得到下图，此时两个数据集的得分基本相当：

MNIST 数据集在单层 100 隐藏节点神经网络进行正则化的准确率曲线

通过上图学习曲线可见，模型在测试数据集上表现良好，在训练准确率曲线与交叉验证准确率之间，存在着相对较小差距，模型对训练数据有些微过拟合，可以继续微调 alpha 值来解决。实际上对于 MNIST 数据集在最终阶段可以看到测试集准确率还在不停上升，所以扩充数据集是一种明显提升准确率的可行方式。

我们可以将防止欠拟合和过拟合的方法总结如下：

• 欠拟合：判断标准：训练集得分较低；增加模型复杂度，降低正则化参数，减少训练集数据（过少的数据集不能正确反映整体数据分布特征），根据测试集得分进行早停。
• 过拟合：判断标准：训练集得分很高，测试集得分低；降低模型复杂度，增加正则化参数，特征选择，增加数据，根据测试集得分进行早停。

验证曲线是一种通过定位过拟合或欠拟合来帮助寻找提高模型性能的参数的方法。验证曲线与学习曲线相似，不过绘制的不是样本大小与训练准确率、测试准确率之间的函数关系，而是准确率与模型参数之间的关系，比如正则化参数 alpha ，神经网络隐藏节点数等与准确率的关系。

这里尝试绘制准确率与隐藏神经元个数的验证曲线，显然我们不应该想当然地来设置隐藏神经元就是 100，而是要根据目标数据集进行验证：

MNIST 数据集准确率和隐藏神经元个数曲线

显然大约 40 个神经元就已经使得训练集达到了过拟合状态，更复杂的神经网络除了增加运算量之外并不能提高准确率。

通过 Pipeline 类结合 scikit-learn 中的学习曲线评估模块 learning_curve 可以很方便地绘制各类学习曲线，这样就无需对不同任务编写大量重复代码：

from sklearn.neural_network import MLPClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn import datasets

def sklearn_learning_curve():
    from sklearn.model_selection import learning_curve

    # 创建神经网络模型
    mlp = MLPClassifier(hidden_layer_sizes=(3,), max_iter=10000, activation='relu',
                        solver='lbfgs', early_stopping=False, verbose=1, tol=1e-6,
                        shuffle=True, learning_rate_init=0.001, alpha=0)

    # 加载IRIR数据集
    pipelr = Pipeline([('scl', StandardScaler()),
                       ('clf', mlp)])

    iris = datasets.load_iris()
    X_train = iris.data
    y_train = iris.target

    # 获取交叉验证数据
    train_sizes, train_scores, valid_scores = \
        learning_curve(estimator=pipelr, X=X_train,y=y_train,
                       train_sizes=np.linspace(0.1, 1, 10, endpoint=True),
                       cv=5, n_jobs=8)

    # 计算交叉验证的平均得分
    train_mean = np.mean(train_scores * 100, axis=1)
    train_std = np.std(train_scores * 100, axis=1)
    valid_mean = np.mean(valid_scores * 100, axis=1)
    valid_std = np.std(valid_scores * 100, axis=1)

    # 绘制曲线图，使用标准差以颜色标记结果的稳定性
    plt.title('IRIS Data Learning Curve')
    plt.plot(train_sizes, train_mean, color='black', marker='o', label='Train Scores')
    plt.fill_between(train_sizes, train_mean + train_std, train_mean - train_std,
                     alpha=0.2, color='black')
    plt.plot(train_sizes, valid_mean, color='purple', marker='s', label='Validation Scores')
    plt.fill_between(train_sizes, valid_mean + valid_std, valid_mean - train_std,
                     alpha=0.2, color='purple')
    plt.xlabel('Trainset samples')
    plt.ylabel('Scores')
    plt.legend(loc='lower right')
    plt.grid()
    plt.show()

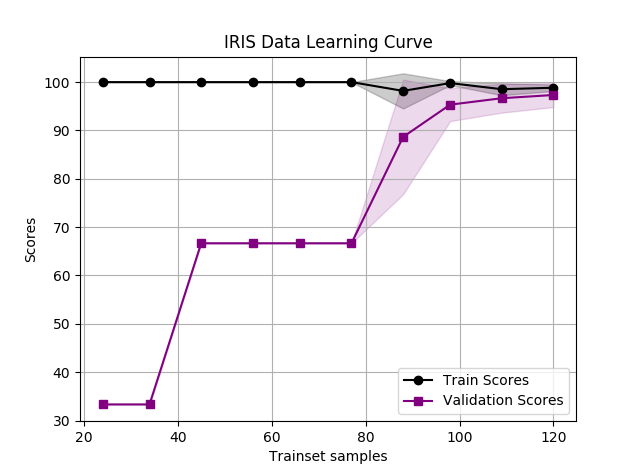
这里使用 IRIS 数据训练隐藏层节点为 3 个的神经网络，由于分类只有 3 中，且数据量不大，采用 3 个隐层节点的神经网络已经足够，这里使用 lbfgs 加速小批量数据的梯度下降，cv=5 表示 5 折（Stratified）交叉验证，最终得到如下学习曲线：

IRIS 数据集准确率学习曲线

实际上通过交叉验证，验证集上准确率已经达到了 98%，即便使用 2 个隐层节点的神经网络依然可以达到如此准确度，可见神经网络的学习能力非常强。

sklearn 同样提供了交叉验证曲线的绘制模块，位于 model_selection 中的 validation_curve，注意点在于参数名称的指定，管线分类器名称加两个下划线再加参数名：

def sklearn_validation_curve():
    from sklearn.model_selection import validation_curve

    mlp = MLPClassifier(hidden_layer_sizes=(3,), max_iter=10000, activation='relu',
                        solver='lbfgs', early_stopping=False, verbose=1,
                        tol=1e-6, shuffle=True,
                        learning_rate_init=0.001)

    pipelr = Pipeline([('scl', StandardScaler()),
                       ('clf', mlp)])

    iris = datasets.load_iris()
    X_train = iris.data
    y_train = iris.target

    # 交叉验证的正则化参数
    param_range = (0, 0.001, 0.01, 0.1, 1.0, 10)
    train_scores, valid_scores = \
        validation_curve(estimator=pipelr, X=X_train,y=y_train,
                         param_name='clf__alpha', param_range = param_range,
                         cv=5, n_jobs=8)
    train_mean = np.mean(train_scores * 100, axis=1)
    train_std = np.std(train_scores * 100, axis=1)
    valid_mean = np.mean(valid_scores * 100, axis=1)
    valid_std = np.std(valid_scores * 100, axis=1)

    plt.title('IRIS Data Validation Curve')
    plt.plot(param_range, train_mean, color='black', marker='o', label='Train Scores')
    plt.fill_between(param_range, train_mean + train_std, train_mean - train_std,
                     alpha=0.2, color='black')
    plt.plot(param_range, valid_mean, color='purple', marker='s', label='Validation Scores')
    plt.fill_between(param_range, valid_mean + valid_std, valid_mean - train_std,
                     alpha=0.15, color='purple')
    plt.xlabel('Regulization Parameter \'alpha\'')
    plt.ylabel('Scores')
    plt.legend(loc='lower right')
    plt.grid()
    plt.ylim([80,100])
    plt.xscale('log')
    plt.show()

IRIS 数据集正则参数的验证曲线

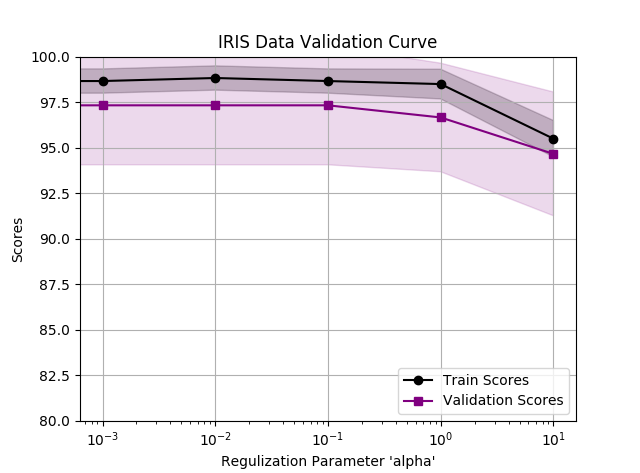
图中可以看出增加正则化参数并不能显著提高校验集分数，并且随着正则化参数的增大，模型趋向于欠拟合，所以这里无需使用正则化参数。

使用 learning_curve 和 validation_curve 除了带来编码方便之外，它自动实现了多进程的支持，可以使用 n_jobs 来进行多核环境的运算提速，n_jobs = -1表示使用所有核加速。

11.3.16. 网格搜索和随机搜索

learning_curve 把不同的比例的训练集作为变量，validation_curve 把模型中的一个参数作为变量。显然一个模型有非常多的超参数需要调整，比如 MPL 模型中的激活函数，正则化参数 alpha，tol 等等。如果要对每个参数均使用以便 validation_curve 绘图将非常繁琐。

网格搜索（grid search）是功能强大的超参数搜索方式，它通过寻找最优的超参值的组合以获得性能模型。网格搜索思想非常简单，对每种参数均与其他参数组合进行暴力穷举搜索（Brute force parameter search），显然这种计算量是巨大的，适应于小型数据集，或者对大型数据集进行抽样处理，以获得一个大概的参数范围和调优方向。

def sklearn_grid_search():
    from sklearn.grid_search import GridSearchCV
    mlp = MLPClassifier(hidden_layer_sizes=(3,), max_iter=10000, activation='relu',
                        solver='lbfgs', early_stopping=False, verbose=1,
                        tol=1e-6, shuffle=True,
                        learning_rate_init=0.001)

    pipelr = Pipeline([('scl', StandardScaler()),
                       ('clf', mlp)])

    iris = datasets.load_iris()
    X_train = iris.data
    X_labels = iris.target

    # 构造参数网格
    alpha_range = (0, 0.001, 0.01, 0.1, 1.0, 10)
    tol_range = (1e-3, 1e-4, 1e-5, 1e-6, 1e-7)
    act_range = ('relu', 'logistic')
    solver_range = ('lbfgs', 'sgd', 'adam')
    param_grid = {'clf__alpha': alpha_range,
                  'clf__tol': tol_range,
                  'clf__activation': act_range,
                  'clf__solver': solver_range}
    gsclf = GridSearchCV(estimator=pipelr,
                         param_grid=param_grid,
                         scoring='accuracy',
                         cv=5,
                         n_jobs=-1)
    gsclf.fit(X_train, X_labels)

    # 打印最优得分和最优参数
    print(gsclf.best_score_)
    print(gsclf.best_params_)

    # 使用最优模型对测试集进行评估
    bestclf = gsclf.best_estimator_
    bestclf.fit(X_train, X_labels)

    return bestclf

sklearn_grid_search()

>>>
0.98
{'clf__activation': 'relu', 'clf__alpha': 0.001, 'clf__solver': 'lbfgs', 'clf__tol': 0.001}

由于网格搜索进行穷举暴力搜索，所以计算成本相当昂贵，另一种轻量级的方法就是随机搜索（randomized search），sklearn 提供了 RandomizedSearchCV 类，使用它可以以特定的代价从抽样分布中抽取出随机的参数组合。与网格搜索类似，通过字典指定参数搜索空间，这一空间可以是连续的：

def sklearn_random_search():
    from time import time
    from scipy.stats import randint as sp_randint
    from sklearn.model_selection import RandomizedSearchCV
    from sklearn.datasets import load_digits
    from sklearn.ensemble import RandomForestClassifier

    # get some data
    digits = load_digits()
    X, y = digits.data, digits.target

    # build a classifier
    clf = RandomForestClassifier(n_estimators=20)

    # Utility function to report best scores
    def report(results, n_top=3):
        for i in range(1, n_top + 1):
            candidates = np.flatnonzero(results['rank_test_score'] == i)
            for candidate in candidates:
                print("Model with rank: {0}".format(i))
                print("Mean validation score: {0:.3f} (std: {1:.3f})".format(
                      results['mean_test_score'][candidate],
                      results['std_test_score'][candidate]))
                print("Parameters: {0}".format(results['params'][candidate]))
                print("")

    # specify parameters and distributions to sample from
    param_dist = {"max_depth": [3, None],
                  "max_features": sp_randint(1, 11),
                  "min_samples_split": sp_randint(2, 11),
                  "bootstrap": [True, False],
                  "criterion": ["gini", "entropy"]}

    # run randomized search
    n_iter_search = 20
    random_search = RandomizedSearchCV(clf, param_distributions=param_dist,
                                       n_iter=n_iter_search, cv=5)

    start = time()
    random_search.fit(X, y)
    print("RandomizedSearchCV took %.2f seconds for %d candidates"
          " parameter settings." % ((time() - start), n_iter_search))
    report(random_search.cv_results_)

以上示例来自 sklearn 的官网，sp_randint 用于生成随机均匀离散分布数据，n_iter 是一个比较重要的参数，选择随机测试参数组合的数量，越大耗时越久，但是尝试的参数越多，效果越好。连续空间需要 scipy 概率统计模块的支持，详细参考 scipy.stats 模块的使用，例如连续指数分布：scipy.stats.expon(scale=100) 可以用于正则化参数的搜索。